Предмет: Алгебра,
автор: vladamiksakova014
помогите срочно дам 35 баллов
Приложения:
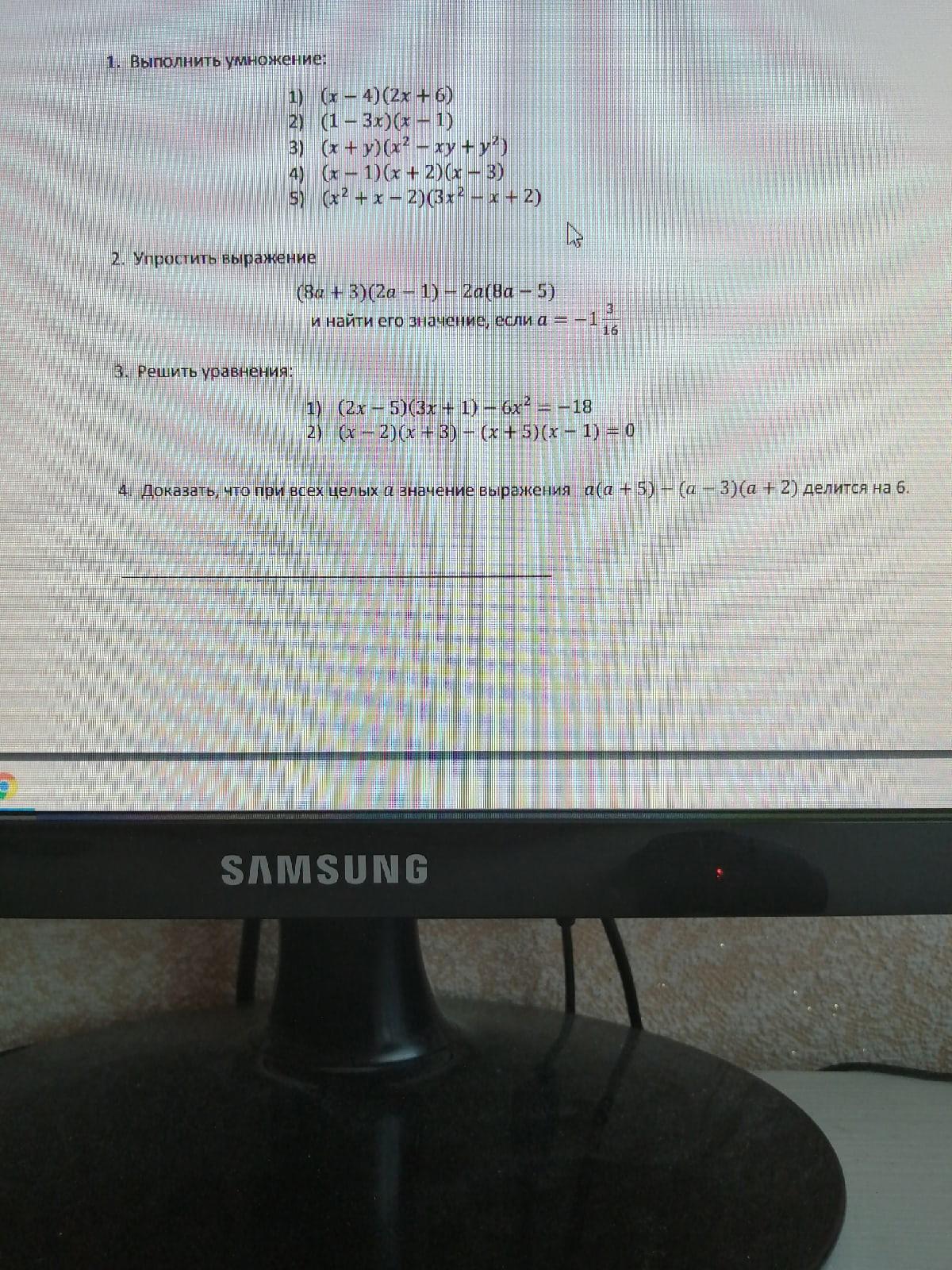
Ответы
Автор ответа:
1
Объяснение:
1.
Номера 2.; 3.; 4. - см. в приложенных файлах
Приложения:



Похожие вопросы
Предмет: Английский язык,
автор: Nurinika
Предмет: Русский язык,
автор: аня4545
Предмет: Английский язык,
автор: Olegtiger
Предмет: Геометрия,
автор: xaili02
Предмет: Химия,
автор: cuddlesann08