Предмет: Алгебра,
автор: mta5572021
ПОЖАЛУЙСТА ВЫЧИСЛИТЕ СРОЧНО
Приложения:
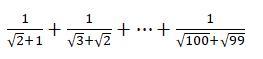
Ответы
Автор ответа:
0
Ответ:
9
Объяснение:
тогда
Похожие вопросы
Предмет: Русский язык,
автор: лена139
Предмет: Другие предметы,
автор: владосик7
Предмет: Русский язык,
автор: Артём199515
Предмет: Математика,
автор: Yana0vais
Предмет: Химия,
автор: Денчик0079