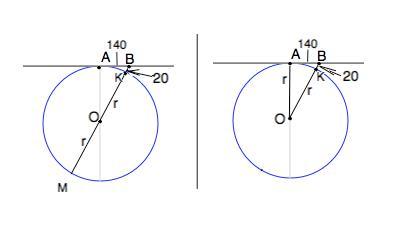
Окружность касается прямой, проведенной через точки A и B, в точке A. Длина отрезка AB равна 140 см., а наименьшее расстояние от точки B до точек окружности составляет 20 см. Найдите радиус окружности.
Ответы
Ответ:
Объяснение:
Проведем из т. В через центр О окружности прямую. Пересечением этой прямой с окружностью будут точки К и М.
КМ = диаметр, ВК - наименьшее расстояние от т.В до точек окружности, ВМ - наибольшее расстояние.
АВ – касательная, ВМ - секущая, – ее длина равна сумме длин диаметра окружности и внешней части секущей:
ВМ=МК+КВ=2r+20
Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной. (Теорема).
ВМ•ВК = АВ²
(2r+20)•20=19600
40r=19600-400=19200 ⇒
r=19200:40=480 (см)
———
Вариант решения:
Радиус, проведенный в точку касания с прямой, перпендикулярен ей. Поэтому ∆ АОВ - прямоугольный.
АО=r; BO=r+20; AB=140 .
По т.Пифагора ВО^2-АО^2=АВ^2.
(r+20)²-r²=19600. Решив уравнение, получим r=480 (см)