Предмет: Алгебра,
автор: mandarinka02052009
Помогите, пожалуйста с этим номером.
Приложения:
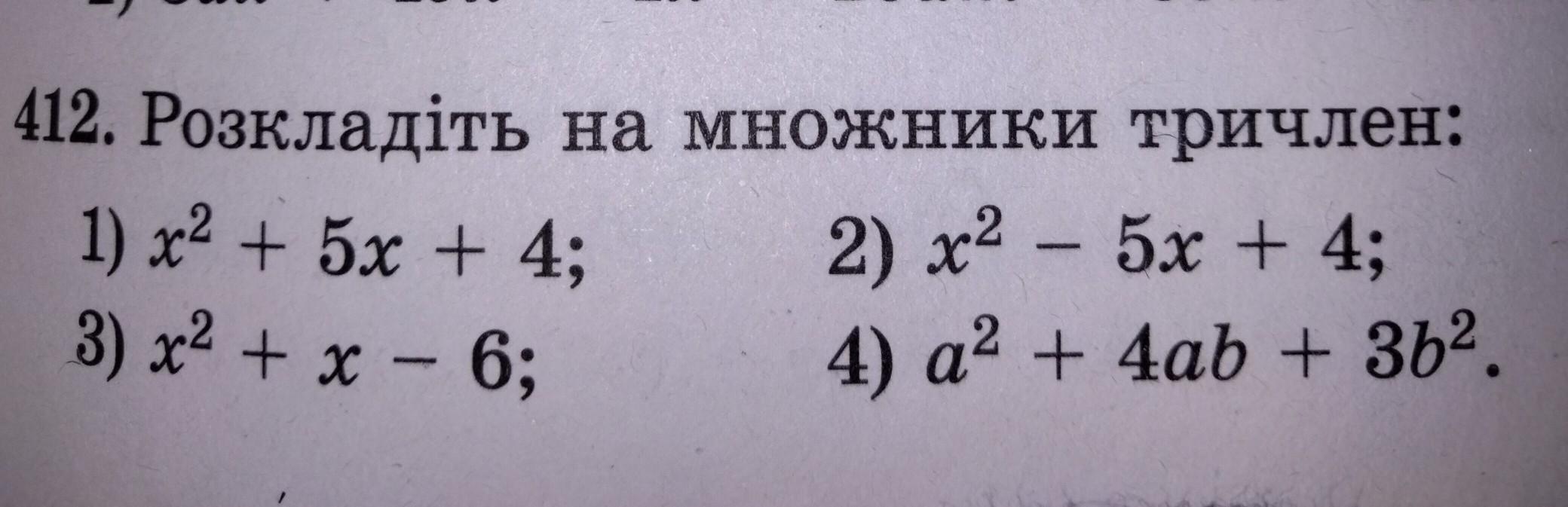
Ответы
Автор ответа:
0
Ответ:
Решай через дискриминант, что там сложного?
mandarinka02052009:
ты мне америку открыл, гений
ага
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ermekovaaysha
Предмет: Русский язык,
автор: SimkaOwl
Предмет: Русский язык,
автор: Diko101
Предмет: Экономика,
автор: anyaalekseeva3
Предмет: Алгебра,
автор: carrot4