Предмет: Алгебра,
автор: sloki1407
решите систему уравнений
Приложения:
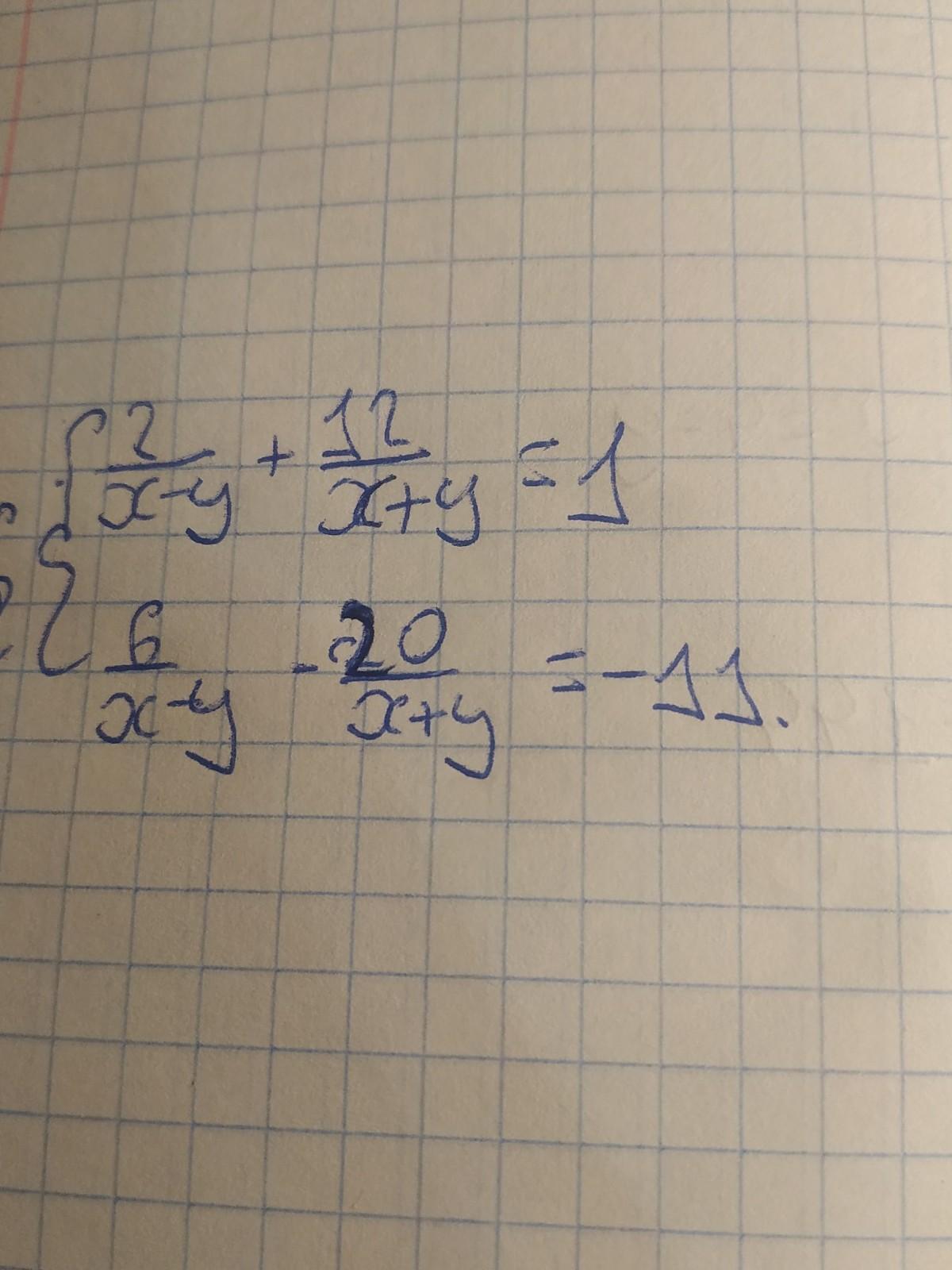
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Денчик109
Предмет: Русский язык,
автор: максим1333
Предмет: Русский язык,
автор: fjihahsjbdkskabv
Предмет: Обществознание,
автор: den4ik2085