Question

помогите пожалуйста, 70 баллов​

Answer 1

Ответ:

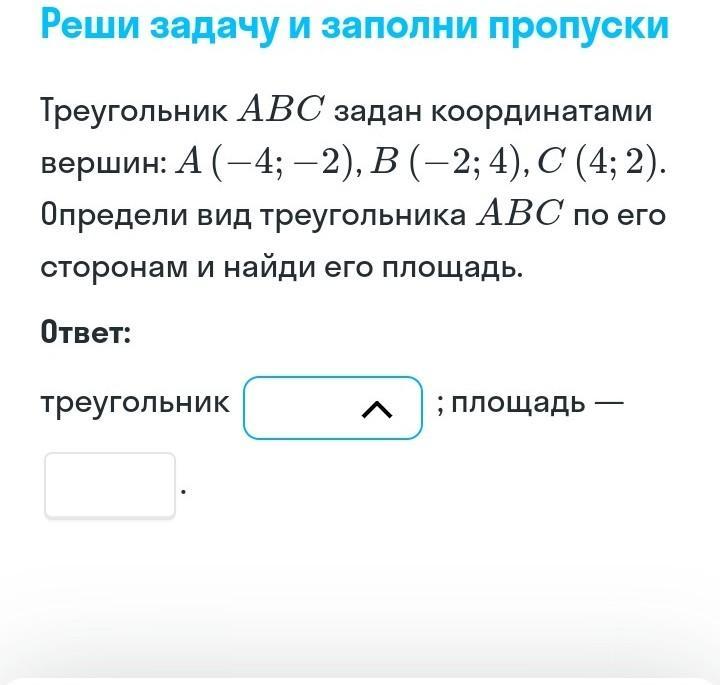
Треугольник АВС - прямоугольный равнобедренный,

с равными катетами АВ и ВС и гипотенузой АС

Площадь треугольника АВС равна

$S_{ABC} = 20$

Объяснение:

$A(-4;-2), \: B(-2;4), \: C(4;2)$

Найдем длины сторон треугольника АВС:

АВ, АС и ВС.

Длина АВ равна

$|AB|= \sqrt{(B_x-A_x)^2+(B_y-A_y)^2} = \\ = \sqrt{( - 2 - ( - 4))^{2} + (4 - ( - 2)) ^{2} } = \\ = \sqrt{( - 2 + 4)^{2} + (4 + 2) ^{2} } = \sqrt{ {2}^{2} + {6}^{2} } = \\ = \sqrt{4 + 36} = \sqrt{40} = 2 \sqrt{10}$

Длина ВС равна

$|BC|= \sqrt{(C_x-B_x)^2+(C_y-B_y)^2} = \\ = \sqrt{( 4 - ( - 2))^{2} + (2- 4) ^{2} } = \\ = \sqrt{( 4+2)^{2} + (2-4) ^{2} } = \sqrt{ {6}^{2} + (-2)^{2} } = \\ = \sqrt{ 36+4} = \sqrt{40} = 2 \sqrt{10} </p><p>$

Длина АС равна

$|AC|= \sqrt{(C_x-A_x)^2+(C_y-A_y)^2} = \\ = \sqrt{( 4 - ( - 4))^{2} + (2- (-2)) ^{2} } = \\ = \sqrt{( 4+4)^{2} + (2+2) ^{2} } = \sqrt{ {8}^{2} + {(4)}^{2} } = \\ = \sqrt{ 64+16} = \sqrt{80} = 4 \sqrt{5}$

Итак мы имеем следующее:

$AB=2\sqrt{10}, \: BC = 2\sqrt{10}; = > \\ = > \: \: AB = BC$

Следовательно, ∆АВС - равнобедренный,

с основанием АС.

Более того, вследствие того, что

$|AB|^2 + |BC|^2 = (2\sqrt{10})^2+(2\sqrt{10})^2 = \\ = 4\cdot10+4\cdot10 = 8\cdot10 =80\\ |AC|^2=(4\sqrt{5})^2=16\cdot5=80 \\ |AB|^2 + |BC|^2 =|AC|^2 \: \: \: = >$

=> ∆ABC - прямоугольный с гипотенузой АС.

А следовательно, площадь прямоугольного треугольника АВС равна половине произведений его катетов АВ и ВС:

$S_{ABC} = \frac{1}{2}\cdot|АВ|\cdot|ВС|=\frac{1}{2}\cdot2\sqrt{10}\cdot2\sqrt{10}= \\ = \frac{1}{2}\cdot4\cdot10=2\cdot10 = 20$