Question

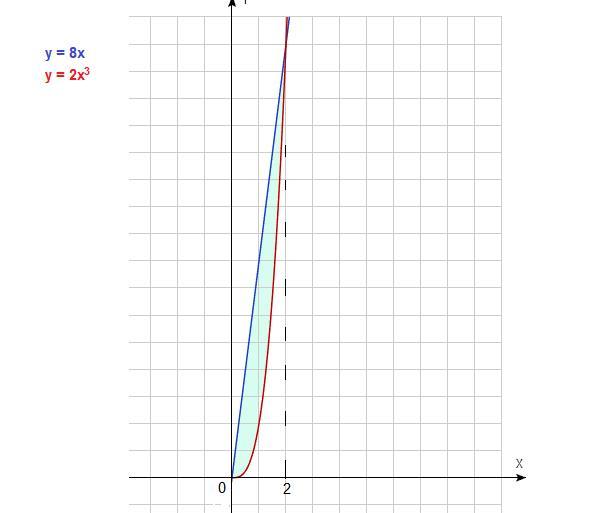
Найдите объём тела, образованного вращением около оси абсцисс фигуры, ограниченной прямой y = 8x и графиком функции y = 2x^3 при x ≥ 0. Выполните рисунок.

Answer 1

Ответ:

$V=\dfrac{2048\pi }{21}$

Объяснение:

Объем тела, образованного вращением около оси абсцисс фигуры, ограниченной графиком функции y = f(x), находится по формуле:

$V=\int\limits^a_b {\pi f^2(x)} \, dx$

Чтобы найти объем тела, ограниченного графиками двух функций, надо от объема тела, ограниченного верхним графиком, отнять объем тела, ограниченного нижним графиком.

Графики функций y = 8x и  y = 2x³ на рисунке.

Найдем точки пересечения графиков (пределы интегрирования):

$2x^3=8x$

$2x^3-8x=0$

$x(x^2-4)=0$

$x(x-2)(x+2)=0$

$x=0,\; \: x=2,\; \: x=-2$

Так как по условию х ≥ 0, то пределы интегрирования от 0 до 2.

$V=\int\limits^2_0 {\pi (8x)^2} \, dx -\int\limits^2_0 {\pi (2x^3)^2} \, dx =$

$=\int\limits^2_0 {\pi 64x^2} \, dx -\int\limits^2_0 {\pi 4x^6} \, dx =$

$=64\pi \cdot \dfrac{x^3}{3}\bigg|\limits^2_0-4\pi \cdot \dfrac{x^7}{7}\bigg|\limits^2_0=\pi \cdot \dfrac{2^6\cdot 2^3}{3}-\pi\cdot \dfrac{2^2\cdot 2^7}{7}=$

$=2^9\cdot \pi \cdot \left(\dfrac{1}{3}-\dfrac{1}{7}\right)=\dfrac{2^9\cdot \pi\cdot 4}{21}=\dfrac{2048\pi}{21}$

$\boldsymbol{V=\dfrac{2048\pi }{21}}$