Предмет: Алгебра,
автор: isakovainna23
Решите, пожалуйста, уравнение, желательно с подробным решением.
Приложения:
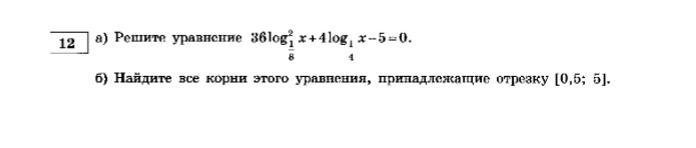
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: ИванХарченко
Предмет: Английский язык,
автор: Artem1918
Предмет: Українська література,
автор: svetagela1980
Предмет: Математика,
автор: ольга1650
Предмет: Русский язык,
автор: nadyushkaartem