Предмет: Геометрия,
автор: dimasss373838
Помогите плиз с 3 заданием
Приложения:

dimasss373838:
Есть пример такого задания
Ответы
Автор ответа:
1
Объяснение:
Дано :
ABCD - квадрат
Найти :
Решение :
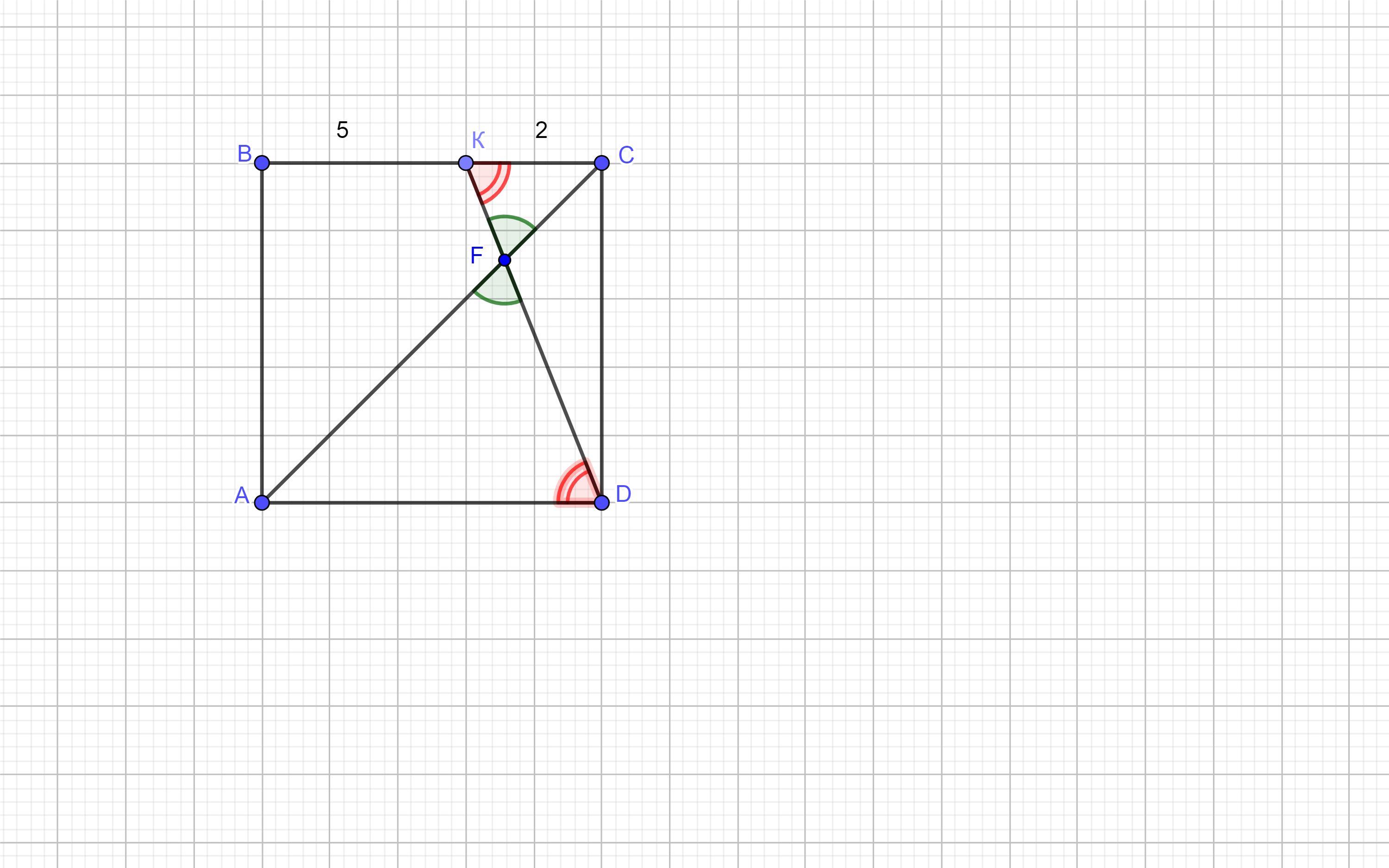
Построим квадрат ABCD, на стороне ВС отметим т.К и проведем отрезки АС и KD ( рисунок во вложении) .
Пусть сторона ВС равна х, тогда ВС= ВК + КС = 5х+2х = 7х
Так как ABCD - квадрат , то ВС = AD = 7x
Рассмотрим ΔKFC и ΔADF.
В этих треугольниках ∠KFC =∠AFD так как вертикальные .
∠CKF = ∠ADF как внутренние накрест лежащие
соответственно ΔADF подобен ΔCFK по первому признаку подобия .
Тогда отношение , где
k - коэффициент подобия/
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия, следовательно
Ответ :
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: TEPEBOHKA
Предмет: Русский язык,
автор: rybalova1984
Предмет: Английский язык,
автор: 194535
Предмет: Математика,
автор: Masha8811
Предмет: Литература,
автор: annostapenk12