Предмет: Геометрия,
автор: Lenorman
две вершины параллелограмма соединили с серединами его сторон так как показано на рисунке 14 полученные два отрезка пересекаются в точке о. в каком отношении точка о делит каждый из них? срочно блллл
Приложения:

Ответы
Автор ответа:
4
Ответ:
Объяснение:
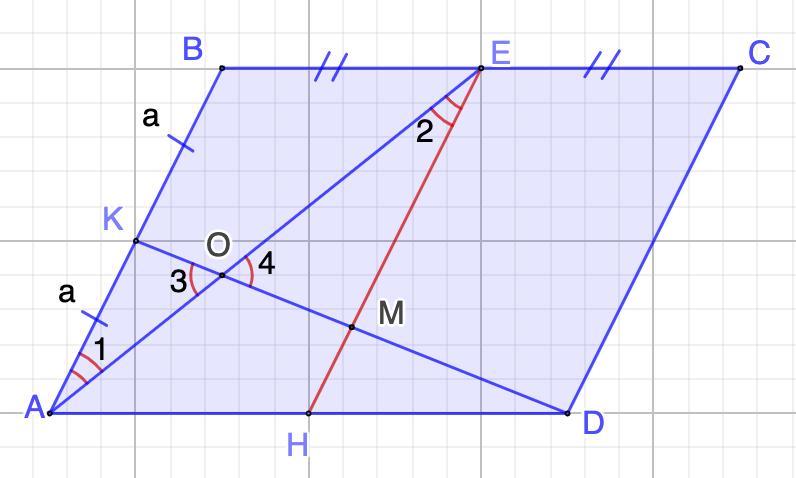
Дано: ABCD - параллелограмм.
АК = КВ; ВЕ = ЕС.
Найти: KO : OD; AO : OE.
Решение:
Проведем ЕН || АВ
⇒ АВЕН - параллелограмм (по определению)
⇒ АН = НD
- Противоположные стороны параллелограмма равны.
⇒ ВC = AD; ВЕ = АН ⇒ АН = НD
1. Рассмотрим ΔАКD.
АН = НD; AK || HM
- Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
⇒ НМ - средняя линия.
Пусть АК = КВ = а.
- Средняя линия равна половине основания.
2. Рассмотрим ΔАКО и ΔОЕМ.
∠1 = ∠2 ( накрест лежащие при АВ || НЕ и секущей АЕ)
∠3 = ∠4 (вертикальные)
⇒ ΔАКО ~ ΔОЕМ (по двум углам)
Составим отношение сходственных сторон:
3. КМ = МD (НМ - средняя линия ΔАКD)
Пусть КО = 2х, тогда ОМ = 3х ⇒ КМ = МD = 5x.
OD = 3x + 5x = 8x
Получим:
KO : OD = 1 : 4; AO : OE = 2 : 3.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: katya586
Предмет: Русский язык,
автор: nurgul1983
Предмет: Русский язык,
автор: Ардоас
Предмет: Қазақ тiлi,
автор: mamasita8000