Помогите пожалуйста. Мой вариант №10. Буду благодарен если поможете всем чем сможете ))). Первый пункт уже сделан
A1 (7,7,3) A2 (6,5,8) A3 (3,5,8) A4 (8,4,1)

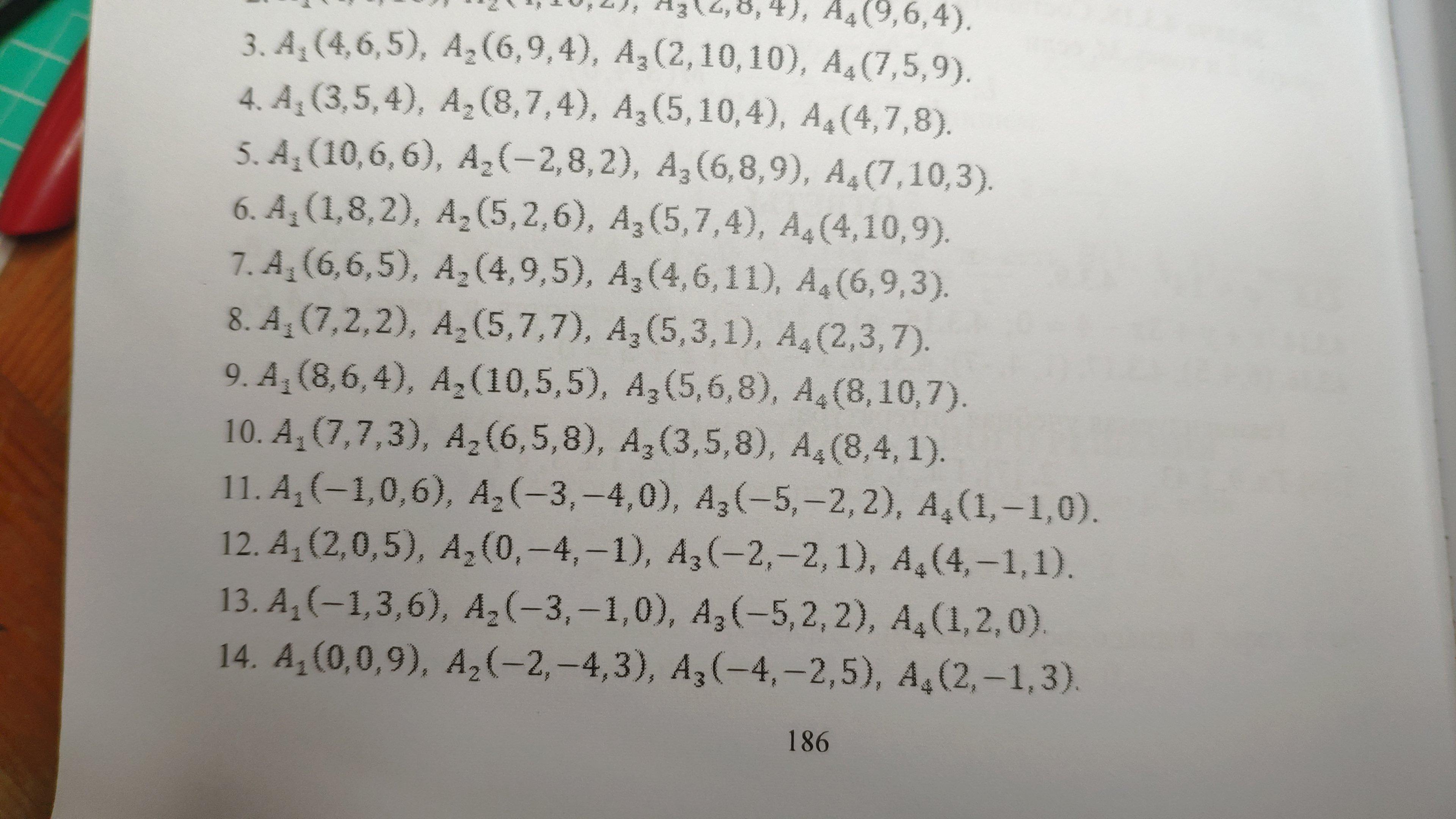
Ответы
Даны точки A1(7,7,3), A2(6,5,8), A3(3,5,8), A4(8,4,1).
1) Находим векторы.
Вектор А1А2 = (6-7; 5-7; 8-3) = (-1; -2; 5),
модуль равен √((-1)² + (-2)² + 5²) = √(1 + 4 + 25) = √30.
Вектор А1А3 = (3-7; 5-7; 8-3) = (-4; -2; 5).
модуль равен √((-4)² + (-2)² + 5²) = √(16 + 4 + 25) = √45 = 3√5.
Также находим вектор А1А4 = (8-7; 4-7; 1-3) = (1; -3; -2).
модуль равен √(1² + (-3)² + (-2)²) = √(1 + 9 + 4) = √14.
Находим нормальный вектор плоскости А1А2А3 как векторное произведение векторов А1А2 и А1А3 с применением схемы Саррюса.
I j k| I j
-1 -2 5| -1 -2
-4 -2 5| - 4 -2 = -10i - 20j + 2k – (-5)j – (-10)i - 8k = 0i - 15j - 6k.
Получили нормальный вектор плоскости (0; -15; -6).
Можно принять коллинеарный ему вектор (0; 15; 6).
Угол между прямой и плоскостью находим по формуле:
sin φ = | A · l + B · m + C · n |
√(A² + B² + C²)· √(l² + m² + n²)
Подставим данные и найдём угол.
∠(A1А4,A1А2А3)=arcsin|⟨A1А4→,n⃗ А1А2А3⟩||A1А4→|⋅|n⃗ А1А2А3| =
=arcsin |1⋅0+(−3)⋅15+(−2)⋅6 |____
√(1²+(−3)²+(−2)²)⋅√(0²+15²+6²) =
arcsin(19√406/406)≈1.231 радиан = (1.231⋅180π)∘≈70.554°.
2) Для составления уравнения плоскости А1А3А4 используем формулу:
x - xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA = 0
Подставим данные и упростим выражение:
x – 7 y – 7 z – 3
3 – 7 5 – 7 8 – 3
8 – 7 4 – 7 1 - 3 = 0
x – 7 y – 7 z – 3
-4 -2 5
1 -3 -2 = 0
(x – 7)(-2·(-2)-5·(-3)) – (y – 7)((-4)·(-2)-5·1) + (z – 3)((-4)·(-3)-(-2)·1) = 0
19(x – 7) + (-3)(y – 7) + 14(z – 3)= 0
19x - 3y + 14z - 154 = 0.
Нормальный вектор плоскости равен (19; -3; 14).
Для составления уравнения плоскости А2А3А4 используем ту же формулу.
Подставим данные и упростим выражение:
x – 6 y – 5 z – 8
3 – 6 5 – 5 8 – 8
8 – 6 4 – 5 1 - 8 = 0
x – 6 y – 5 z – 8
-3 0 0
2 -1 -7 = 0
(x – 6)(0·(-7)-0·(-1)) – (y – 5)((-3)·(-7)-0·2)+ (z – 8)((-3)·(-1)-0·2) = 0
0(x – 6) + (-21)(y – 5) + 3(z – 8) = 0
-21y + 3z + 81 = 0.
Нормальный вектор плоскости равен (0; -21; 3).
Вычислим угол между плоскостями
19x - 3y + 14z - 154 = 0 и - 21y + 3z + 81 = 0
cos α = |A1·A2 + B1·B2 + C1·C2|
√(A1² + B1² + C1²)*√(A2² + B2² + C2²)
cos α = |19·0 + (-3)·(-21) + 14·3|
√(19² + (-3)² + 14²)* √(0² + (-21)² + 3²) =
= |0 + 63 + 42|
√(361 + 9 + 196)*√(0 + 441 + 9) =
= 105/(√566 *√450) = 105/√254700 = 7√283/566 ≈ 0,20805.
α = 77.9917°.
3) Находим вектор А1А2 = (6-7; 5-7; 8-3) = (-1; -2; 5).
Получаем уравнение А1А2:
(x – 7)/(-1) = (y – 7)/(-2) = (z – 3)/5.
8) Нормальный вектор плоскости А1А2А3 уже найден и равен (0; 15; 6).
Осталось подставить координаты точки А1(7; 7; 3) и подставить в уравнение плоскости.
0*(x – 7) + 15*(y – 7) + 6*(z – 3) = 0. Получаем:
15у + 6z – 123 = 0.
9) Для параллельной плоскости коэффициенты переменных в уравнении (а это координаты нормального вектора) сохраняются.
Подставляем координаты точки А4(8; 4; 1).
0*(x – 8) + 15*(y – 4) + 6*(z – 1) = 0. Получаем:
15у + 6z – 66 = 0.
10) Этот вопрос не имеет однозначного решения, так как через одну точку можно провести неограниченное множество плоскостей, перпендикулярных заданной.
11) Находим вектор А1А4 = (8-7; 4-7; 1-3) = (1; -3; -2).
Уравнение прямой А1А4:
(x - 7)/1 = (y – 7)/(-3) = (z – 3)/(-2).
12) Длина высоты – это расстояние от точки А4 до плоскости А1А2А3.
Для вычисления расстояния от точки M(Mx; My; Mz) до плоскости Ax + By + Cz + D = 0
используем формулу:
d = |A·Mx + B·My + C·Mz + D|
√(A² + B² + C²)
Подставим в формулу данные:
d = |0·8 + (-15)·4 + (-6)·1 + 123|
√(0² + (-15)² + (-6)²) =
= 0 - 60 - 6 + 123|
√0 + 225 + 36 =
= 57/√261 = 19√29/29 ≈ 3.52821.
13) Надо найти проекцию точки А4 на плоскость А2А3А4. Пусть это точка Е.
Находим уравнение прямой А4Е.
Нормальный вектор плоскости А2А3А4 найден ранее и равен (0; -21; 3). и является направляющим вектором перпендикуляра к плоскости.
Получаем уравнение перпендикуляра из точки A1(7; 7; 3).
А4Е:((x - 7)/0 = (y - 7)/(-21) = ((z - 3)/3.
Координаты, которые имеет точка Е пересечения x,y,z, должны удовлетворять уравнению прямой и уравнению плоскости. Поэтому, для их определения, необходимо решить систему уравнений, которая включает уравнение прямой и уравнение плоскости. Это система:
{((x - 7)/0 = (y - 7)/(-21) = ((z - 3)/3.
{ -21y + 3z + 81 = 0.
Уравнение прямой представим в параметрическом виде.
((x - 7)/0 = (y - 7/(-21) = ((z - 3)/3 = t,
x - 7 = 0*t , x = 7,
y – 7 = (-21)*t, y = -21t + 7,
z - 3 = 3*t, z = 3t + 3.
Подставим переменные в уравнение плоскости x-y+z+3=0.
-21(-21t + 7) + 3(3t + 3) + 81 = 0,
441t – 147 + 9t + 9 + 81.
450t = 57,
t = 57/450 = 19/150.
Подставим значение t в выражения переменных.
x = 7,
y = -21*(19/150) + 7 = (-399+1050)/150 = 651/150 = 217/50,
z = 3*(19/150) + 3 = (57+450)/150 = 507/150 = 169/50.
Найдена точка E пересечения перпендикуляра из точки A1 и плоскости А2A3A4, она же является проекцией точки A1 на заданную плоскость.
Ответ: Е(7; (217/50); (169/50)).