Предмет: Геометрия,
автор: akazar
СРОЧНО!!! Один з катетів прямокутного трикутника на 4 см менше гіпотенузи , а другий катет дорівнює 12 см.Точка поза площиною трикутника віддалена від кожної з його вершин на 26 см. Знайдіть відстань від даної точки до площини трикутника.
Ответы
Автор ответа:
0
Ответ:
24 см
Объяснение:
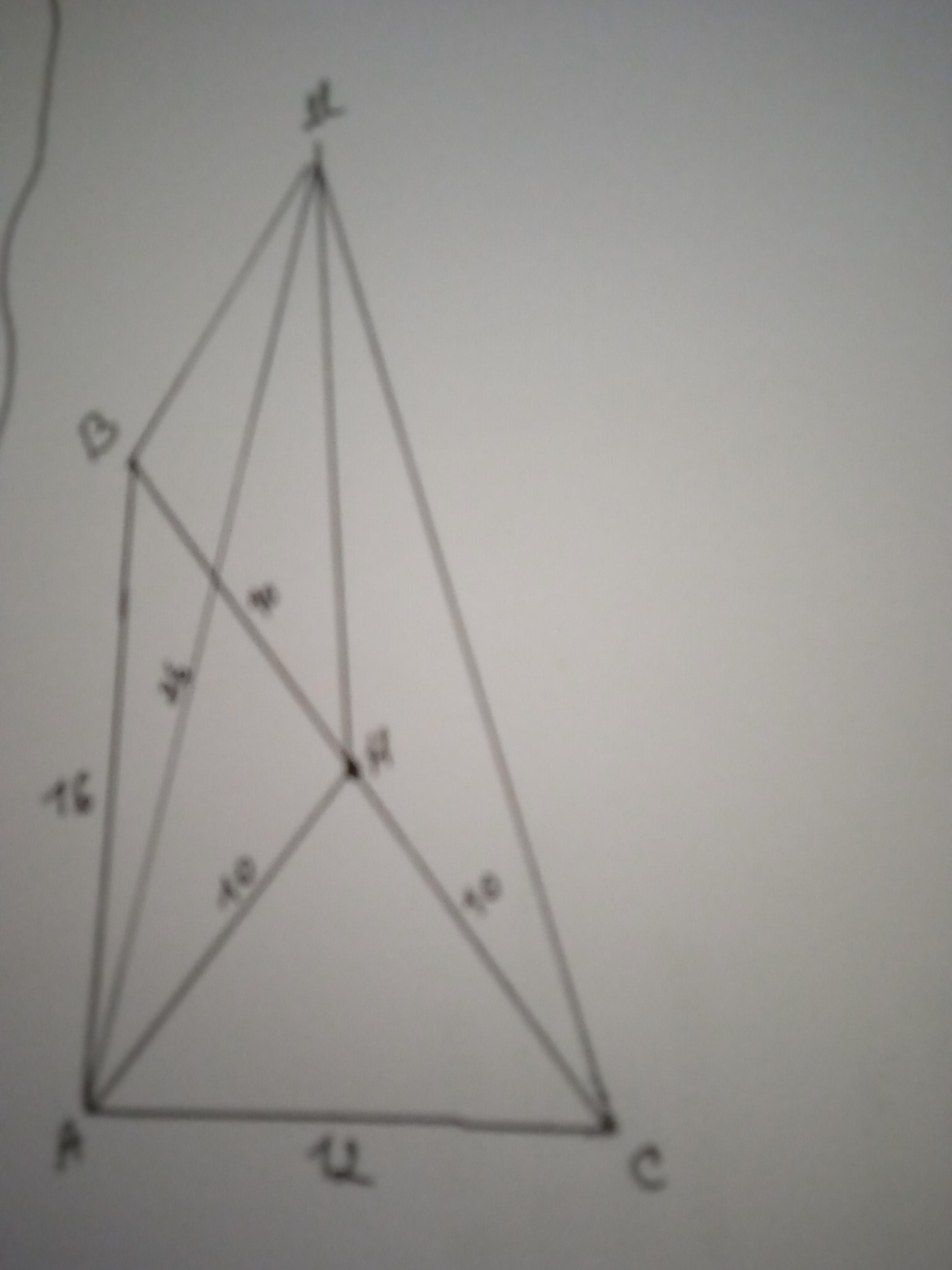
Дано: ΔАВС - прямокутний, ∠А=90°, ВС-АВ=4 см, АС=12 см. ВМ=АМ=СМ=26 см. МН⊥АВС. МН - ?
Якщо точка М віддалена на однакову відстань від усіх вершин ΔАВС, значить, точка Н знаходиться у центрі описаного кола. Центр описаного кола у прямокутного трикутника знаходиться посередині гіпотенузи.
Знайдемо гіпотенузу ВС за теоремою Піфагора:
ВС=х см, АВ=х-4 см
х²=(х-4)²+АС²
х²=х²-8х+16+144
8х=160; х=20
ВС=20 см.
ВН=СН=АН=20:2=10 см (це радіуси описаного кола)
Розглянемо ΔАМН - прямокутний.
МН=√(АМ²-АН²)=√(676-100)=√576=24 см
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: jekgolubnichy
Предмет: Русский язык,
автор: лиля190
Предмет: Русский язык,
автор: деректор2
Предмет: Алгебра,
автор: baghdasarianie
Предмет: Математика,
автор: lenovoleg256