Предмет: Алгебра,
автор: knly
ДАЮ СТО БАЛЛОВ!!!!!! РЕШИТЕ СИСТЕМУ УРАВНЕНИЙ ПОЖАЛУЙСТА!!!!
Приложения:
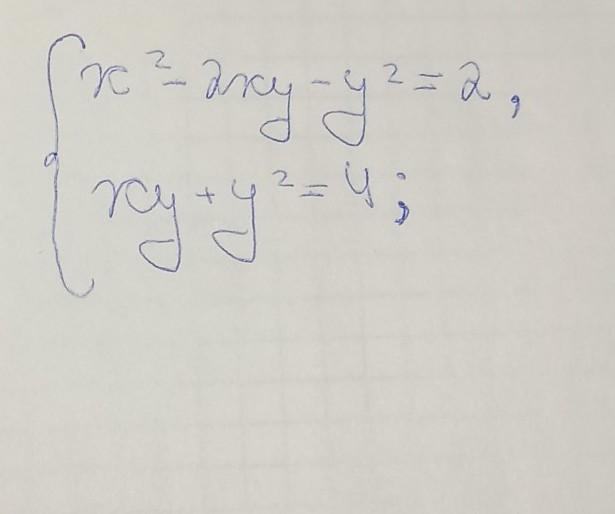
Ответы
Автор ответа:
1
подставим значение х в первое уравнение
Похожие вопросы
Предмет: Окружающий мир,
автор: abakshinaelenaленчк
Предмет: Русский язык,
автор: kapaMeJIka1
Предмет: Русский язык,
автор: kristinakonore113355
Предмет: Литература,
автор: gamenozg
Предмет: Русский язык,
автор: ula60