Предмет: Алгебра,
автор: liza8693000
Решите каких а значение дроби

равно нулю?
Подробнее пожалуйста. Пример решения закреплён.
Приложения:
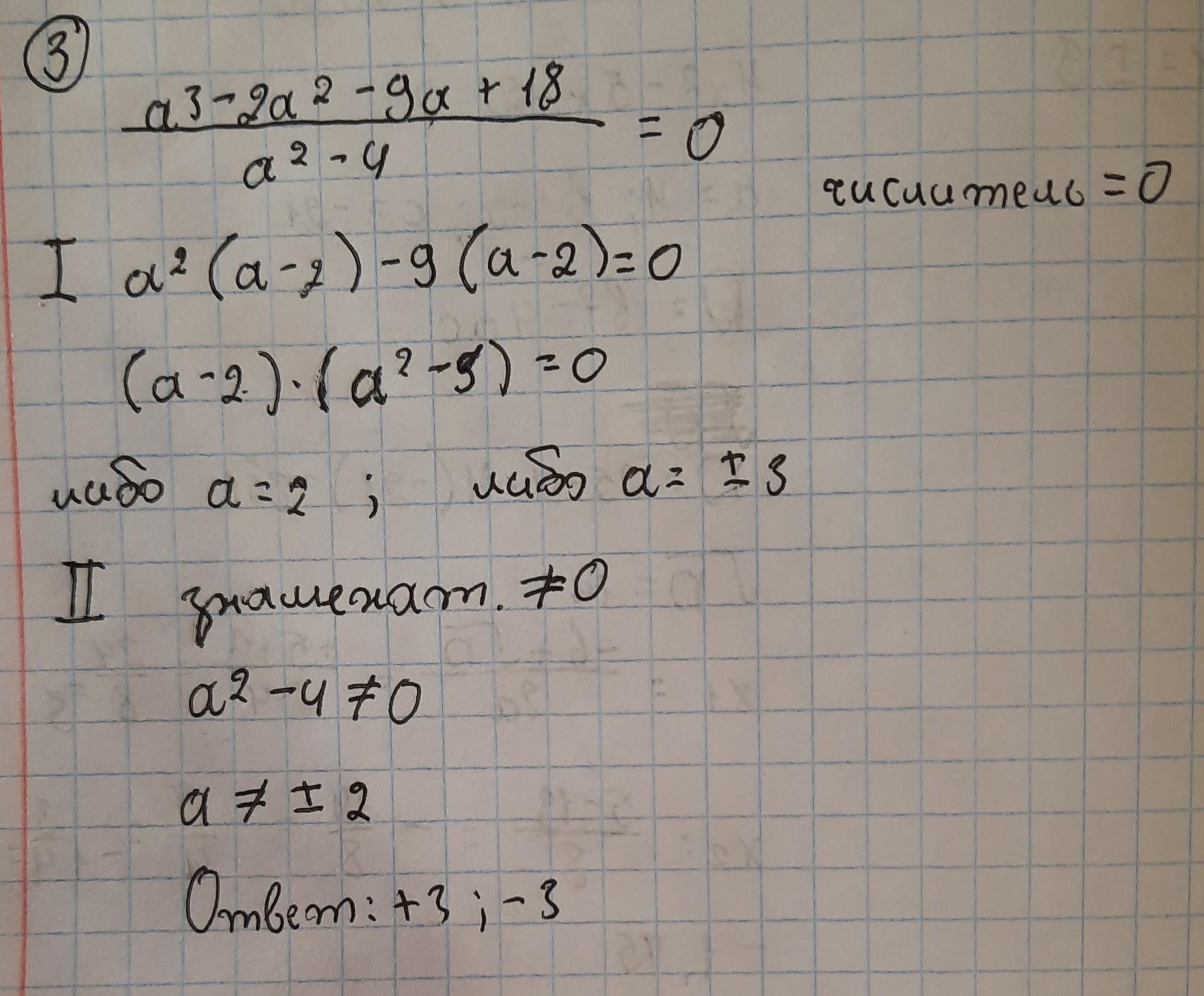
Ответы
Автор ответа:
1
ОДЗ: 
Корень " " нам не подходит, так как не удовлетворяет ОДЗ.
" нам не подходит, так как не удовлетворяет ОДЗ.
OТВЕТ: -6 и 6.
Похожие вопросы
Предмет: Русский язык,
автор: маринка75
Предмет: Немецкий язык,
автор: Вера1997081789
Предмет: Русский язык,
автор: бек21
Предмет: Математика,
автор: Lilo12345678
Предмет: Английский язык,
автор: lizavoroshilova21