Предмет: Математика,
автор: kirilov666o
Решите пожалуйста неравенства
Приложения:
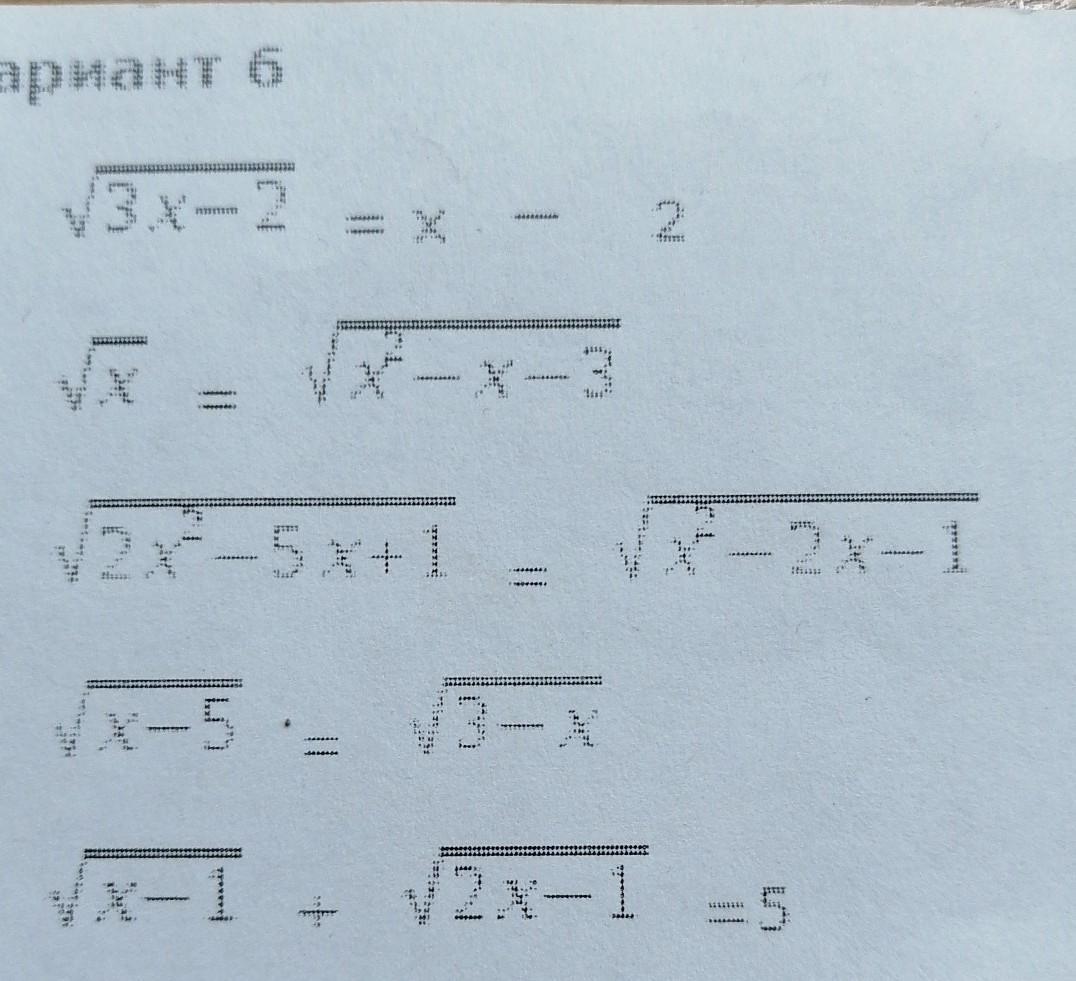
Ответы
Автор ответа:
0
Ответ:
1)
Подставляем в начало:
x=6
2)
x=3
3)
4)
5)
Подставляем в начальное:
x=5
Похожие вопросы
Предмет: Русский язык,
автор: smaylik228
Предмет: Английский язык,
автор: Dan220604
Предмет: Русский язык,
автор: niknat3012mailru
Предмет: Литература,
автор: JeeeK
Предмет: Русский язык,
автор: kuki57