Question

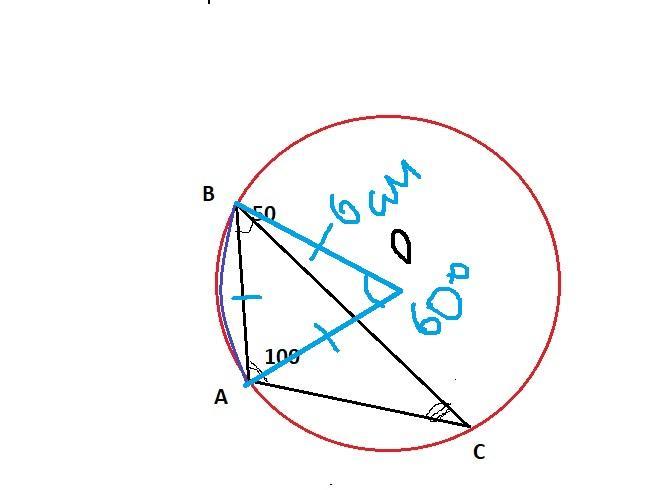
Сторона трикутника дорівнює 6 см, а прилеглi до неї кути дорівнюють 50º i 100°. Вершини трикутника дiлять описане навколо нього коло на три дуги. Знайдіть довжину найменшої дуги​

Answer 1

Відповідь: 2π см або 6,28 см

Пояснення:

Дано :ΔАВС, АВ=6 см, ∠А=100°, ∠В=50°

Знайти: ∪АВ-?

Рішення:

Проти меншого кута лежить менша сторона, отже менший кут спираєтьсяна найменшу дугу.

За теоремою про суму кутів трикутника

∠А+∠В+∠С=180°

100°+50°+∠С=180°

∠С=180°-150°

∠С=30°

Отже ∪АВ- найменша, а ∠С- вписаний кут.

∠ АОВ- центральний- він = 60° (Вписаний кут дорівнює половині центрального кута)∠С=1/2 ∠АОВ →  ∠АОВ=2∠С=2*30°=60°

Розглянемо ΔАОВ, де АО=ОВ= r , ∠АОВ=60°, так як кути при основі рівнобедреного трикутника рівні, то ∠ВАО=∠АВО

2∠ВАО+∠АОВ=180°( за теоремою про суму кутів Δ)

∠ВАО=∠АВО =(180-°60°):2=60°.

Всі кути рівні, отже ΔАОВ- рівносторонній АО=ОВ=АВ=r=6 cм

довжина дуги:

$L=\frac{\pi *r*\alpha }{180^\circ}= \frac{\pi *6*60^\circ}{180^\circ} =2\pi$ (cм)≈2*3,14≈6,28 см