Question

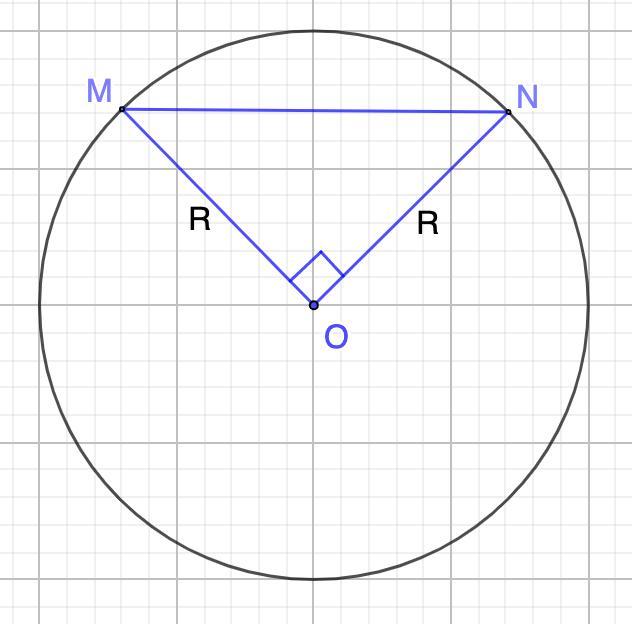
Реши задачу. Дана окружность с центром О и радиусом R. В ней провели хорду MN так, что угол MON — 90°. Чему равен угол MNO?


ЗАРАНЕЕ СПАСИБО​

Answer 1

Ответ:

45°

Объяснение:

Дано: Окр.O,R.

MN - хорда, ∠MON = 90°

Найти: ∠MNO

Решение:

Рассмотрим ΔMNO - прямоугольный.

OM = ON = R

⇒ ΔMNO - равнобедренный.

• В равнобедренном треугольнике углы при основании равны.

⇒ ∠OMN = ∠ONM

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠OMN = ∠MNO = 90° : 2 = 45°