Предмет: Алгебра,
автор: katya106720
Знайти значення виразу. Дам 50 БАЛОВ!!
Приложения:
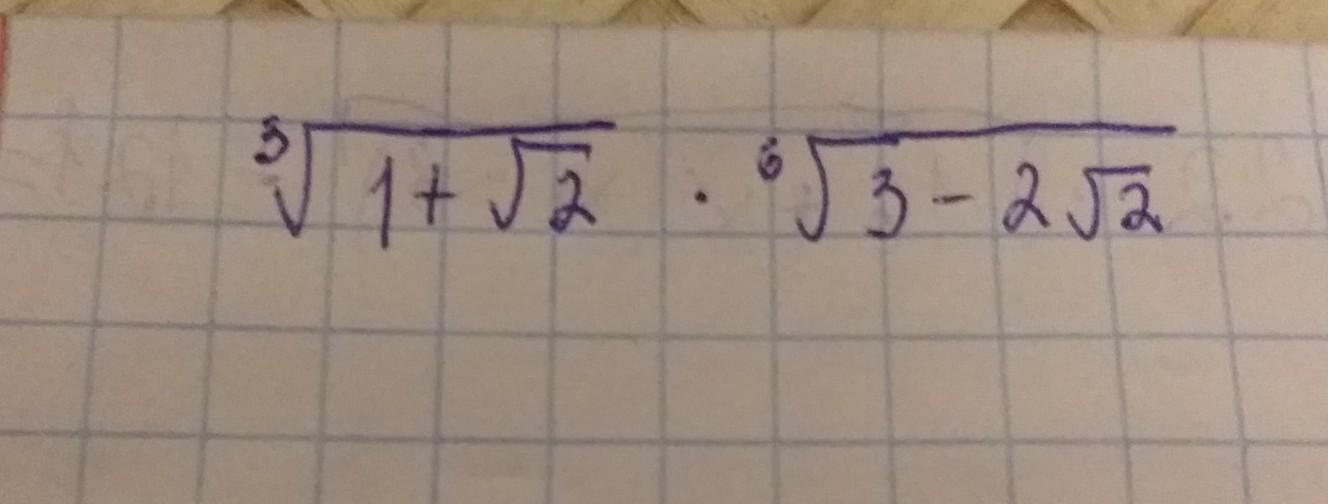
Ответы
Автор ответа:
1
Ответ:
1
Объяснение:
Будут вопросы - задавайте.
Приложения:

katya106720:
СПАСИБО БОЛЬШОЕ
Автор ответа:
1
Первый способ :
Второй способ :
Спасибо ❤
Пожалуйста
Похожие вопросы
Предмет: Русский язык,
автор: lekseytopchiy
Предмет: Русский язык,
автор: gorelikalena
Предмет: Русский язык,
автор: Profi1228
Предмет: Английский язык,
автор: Аноним