Предмет: Математика,
автор: sashhhhkkaa
СРОЧНО СРОЧНО СРОЧНО СРОЧНО
Приложения:
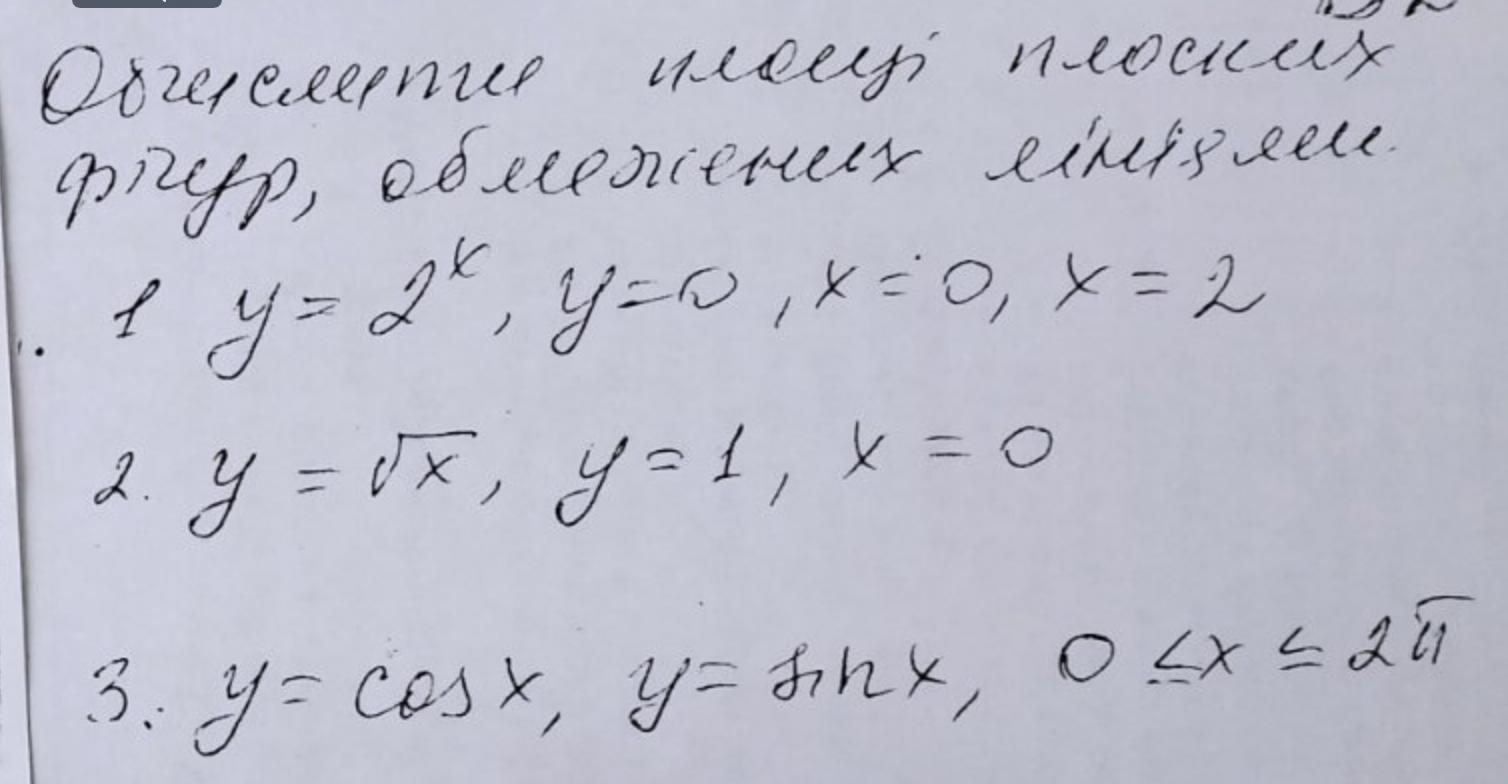
Ответы
Автор ответа:
1
Ответ:
1)
2)
3)
Похожие вопросы
Предмет: Русский язык,
автор: boldness30
Предмет: Русский язык,
автор: 20072203
Предмет: Английский язык,
автор: ДарьяМ11
Предмет: Математика,
автор: наст58