Предмет: Математика,
автор: almasikara
Определи наименьшее натуральное значение, которое является решением неравенства:
x^2 > 38
Ответы
Автор ответа:
2
Ответ:
7.
Пошаговое объяснение:
Решим данное неравенство
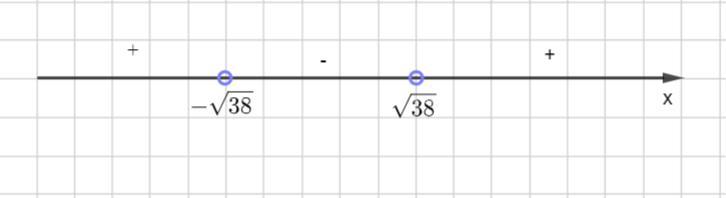
Определим знак функции на каждом из промежутков и получим
при x ∈ (-∞; -√38) ∪(√38; +∞)
Натуральные решения в промежутке (√38; +∞) .
Так 36 < 38 < 49, то
Тогда 7 - наименьшее натуральное число, которое является решением данного неравенства.
Приложения:
drukdila:
все верно, спасибо
Похожие вопросы
Предмет: Другие предметы,
автор: annabel33
Предмет: Английский язык,
автор: alish1993
Предмет: Русский язык,
автор: aska4
Предмет: Русский язык,
автор: Vika77578
Предмет: Геометрия,
автор: viki161718