Предмет: Алгебра,
автор: kirillgranackij
как это решить?
помогите пожалуйста
Приложения:
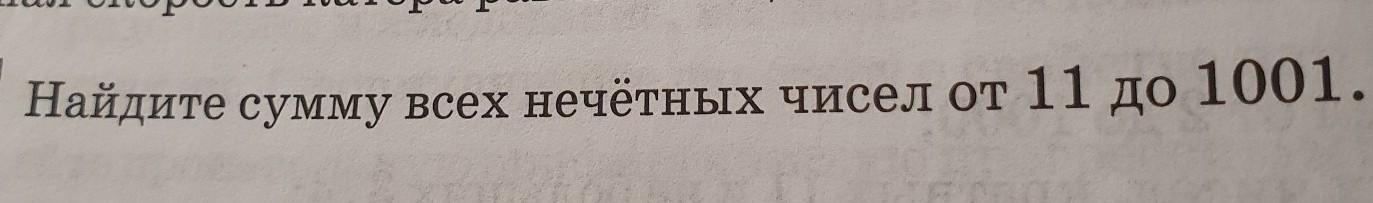
Ответы
Автор ответа:
0
Ответ:
1. Нечетные натуральные числа образуют арифметическую прогрессию A(n), для которой по условию задачи заданы следующие параметры:
первый член A1 = 11;
последний член An = 101;
разность D = 2;
2. Определим номер последнего члена прогрессии по формуле :
An = A1 + D * (n - 1);
n = (An - A1) / D + 1 = (101 - 11) / 2 + 1 = 46;
3. Сумма всех членов прогрессии вычисляется по формуле:
S = ((A1 + An) / 2) * n = ((11 + 101) / 2) * 46 =
56 * 46 = 2576.
Ответ: сумма всех нечетных натуральных чисел от 11 до 101 включительно
Похожие вопросы
Предмет: Русский язык,
автор: олеся0544
Предмет: Русский язык,
автор: олеся0544
Предмет: Другие предметы,
автор: гля
Предмет: Математика,
автор: dilar1234512345
Предмет: Алгебра,
автор: tempmailru