Математика. Нужна помощь
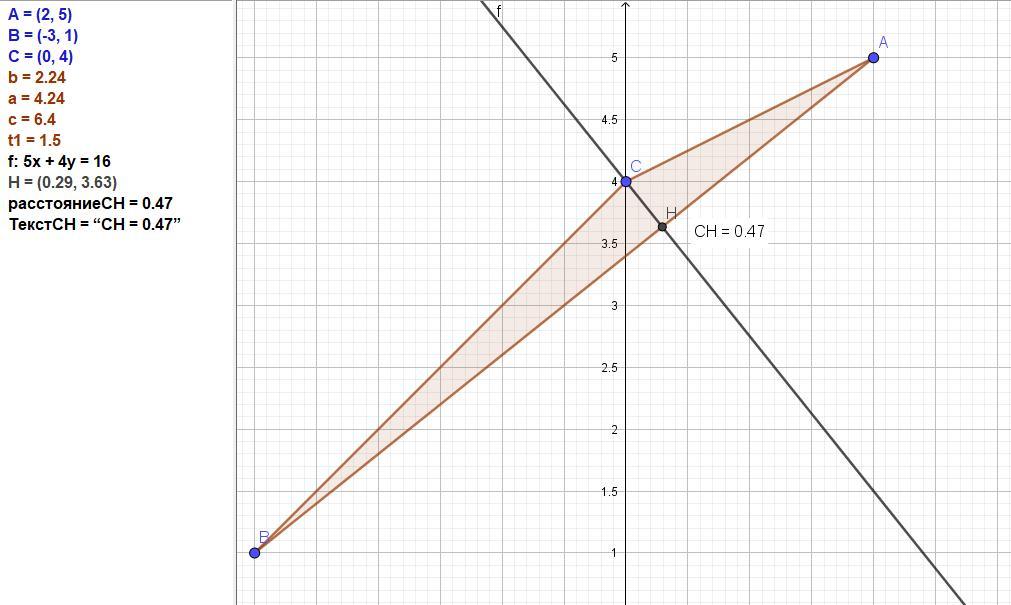
Даны вершины треугольника ABC. A(2,5); B(-3,1); C(0,4)
Найти уравнение стороны AB, уравнение высоты CH.
Уравнение медианы AM
Длину высоты CH
Тангенс A
Уравнение прямой, проходящей через точку C, параллельно стороне AB
Ответы
Даны координаты вершин треугольника ABC: A(2,5); B(-3,1); C(0,4).
Найти:
а) уравнение стороны AB.
Находим вектор АВ = (-3-2; (1-5) = (-5; -4).
Уравнение АВ: (х - 2)/(-5) = (у - 5)/(-4) каноническое.
-4х + 8 = -5у + 25,
4х - 5у + 17 = 0 это общее уравнение АВ.
б) уравнение высоты CH. Это перпендикуляр к стороне АВ.
У перпендикуляра коэффициенты общего уравнения А и В меняются на -В и А (из условия, что их скалярное произведение равно нулю).
Уравнение СН: 5х + 4у + С = 0.
Для определения слагаемого С подставим координаты точки С.
5*0 + 4*4 + С = 0, получаем С = -16.
Уравнение СН: 5х + 4у - 16 = 0.
в) уравнение медианы AM.
Определяем координаты точки М как середины стороны ВС.
М = (B(-3; 1) + C(0; 4))/2 = (-1,5; 2,5).
Вектор АМ = (-1,5-2); 2,5-5) = (-3,5; -2,5).
Уравнение АМ: (х - 2)/(-3,5) = (у - 5)/(-2,5).
Можно привести к целым коэффициентам:
Уравнение АМ: (х - 2)/7 = (у - 5)/5 или в общем виде
5х - 7у + 25 = 0.
г) ) длина высоты СН - это расстояние от точки C(0; 4) до прямой
AB:4х - 5у + 17 = 0.
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = |A·Mx + B·My + C|
√(A² + B²)
Подставим в формулу данные:
d = |4·0 + (-5)·4 + 17|
√(4² + (-5)²)
= |0 - 20 + 17|
√(16 + 25)
= 3
√41
= 3√41 /41 ≈ 0,4685.
д) тангенс угла А определим по разности угловых коэффициентов сторон АВ и АС.
tg AB = Δy / Δx = -4/(-5) = 4/5.
Находим вектор АC = (0-2; (4-5) = (-2; -1).
tg AC = Δy / Δx = -1/(-2) = 1/2.
Отсюда находит tg A по формуле:
tg A = (tg AB – tg AC)/(1 + tg AB*tg AC) = ((4/5) – (1/2))/(1 + (4/5)*(1/2)) = (3/10)/(14/10) = 3/14.
tg A = 3/14.
е) уравнение прямой, проходящей через точку C, параллельно стороне AB, имеет коэффициенты при переменных, равные прямой АВ.
Получаем: СС1 = 4х - 5у + С = 0.
Для определения слагаемого С подставим координаты точки С.
4*0 – 5*4 + С = 0, отсюда С = 20.
Уравнение: 4х - 5у + 20 = 0.