Помогите пожалуйста срочно надо дам 100 баллов за быстрый ответ ;)

Ответы
Ответ:
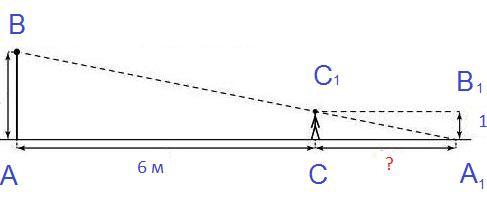
Объяснение: №1. Дано: АС=6 м, АВ=2,7 м, А₁В₁=0,9 м. Найти А₁С.
Решение (см рисунок к задаче):
△АA₁В подобен △CС₁A₁ (по двум углам: ∠ ВА₁А – общий, ∠ВАА₁=∠С₁СА₁=90 °)
В подобных треугольниках соответственные стороны пропорциональны, значит:
АA₁/A₁С=АВ/CC₁
Пусть А₁С=х, тогда АА₁=6+х, СС₁=А₁В₁=0,9
(6+х)/x=2,7/0,9
(6+х)/x=3
6+х=3х
2х=6
х=3 (м) длина тени
№2. Дано:ΔС₁О₁Р₁ подобен ΔСОР, СО=2,5, ОP
=2см, α =60°-угол между ними. k=3 Найти SΔС₁О₁Р₁
Решение: В условии видимо ОР=2 см, у вас с ошибкой записано условие, так как СО=ОС, такого быть не может, я так поняла)
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. т.е.:
S(ΔС₁О₁Р₁ )/ S( ΔСОР) = k² =3²=9.
Найдём площадь ΔСОР:
S(ΔСОР)=( 1/2) ·CO·OP·Sin60° =( 1/2) ·2,5·2·(√3/2) =2,5√3/2= 1,25·√3
тогда S(ΔС₁О₁Р₁ )= S(ΔСОР) ·k² = 1,25√3 ·9=11,25√3.
Ответ: 11,25√3 см²