Все на рисунке!!!!!!!!
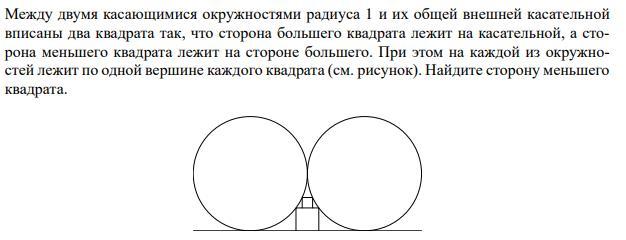
Ответы
Ответ:
Пошаговое объяснение:
!!!!!!!!!!!!!!!!!!!!!!!!!!

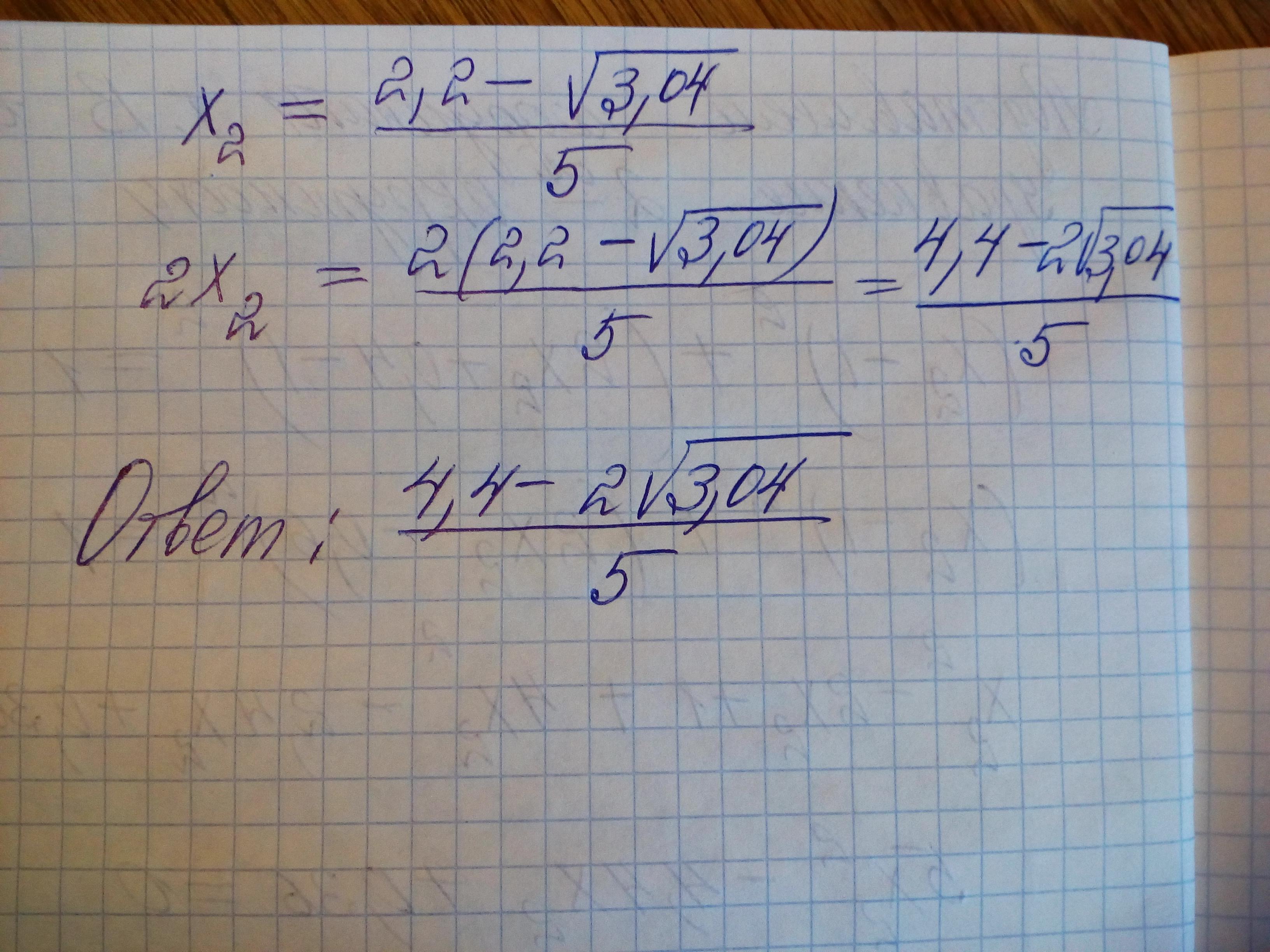
Ответ:
(4,4 - 2√3,04)/5 ед.
Пошаговое объяснение:
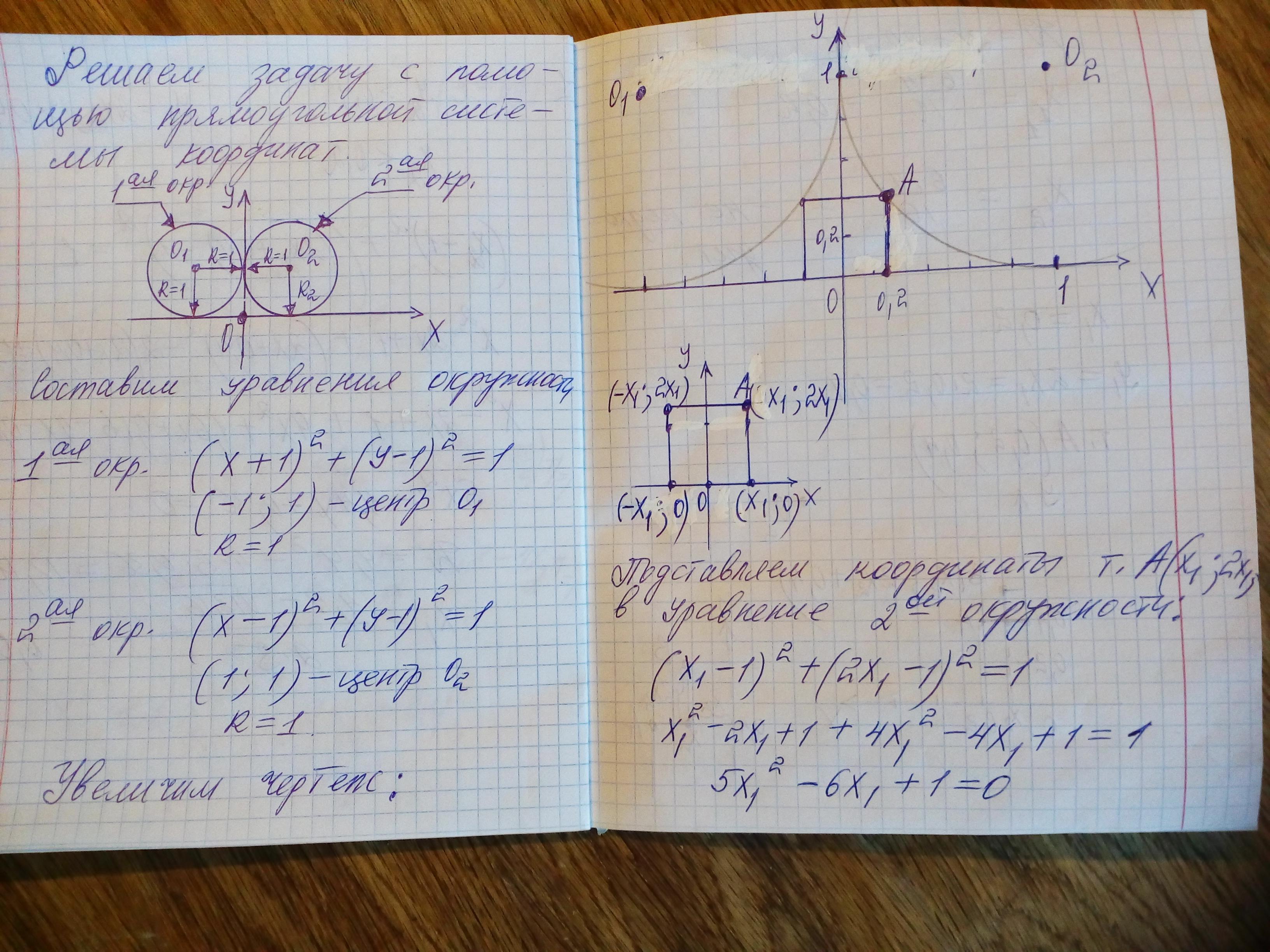
У окружности с центром в точке О (для второй будет аналогично в силу симметричности расположения) проведем диаметр АВ в точку касания с общей касательной НВ и радиус OD в точку касания D двух окружностей. Точку С пересечения общей внешней касательной АВ и касательной, проведенной через точку D касания окружностей примем за начало координат.
Отметим, что касательные к окружностям перпендикулярны радиусам в точках касания и что касательная, проведенная через точку D касания двух равных окружностей перпендикулярна их общей внешней касательной и делит ее отрезок (НВ) пополам в точке пересечения С.
Тогда, соединив точки А диаметра и С (начало координат), получим прямую АС, соответствующую уравнению y = kx + b, где k = AB/CB = 2 (по условию), а b = 0 (по построению).
Итак, уравнение прямой АС: y = 2x. (1)
Уравнение данной нам окружности по условию и построению такое:
(x-1)² + (y-1)² = 1. (2).
Обозначим точкой Е точку пересечения нашей окружности и прямой АС и опустим перпендикуляр ЕК на прямую ВН. Тогда ЕК = 2·EG (в силу подобия треугольников АВС и ЕКС), ∠ЕНС = ∠KEG = 90° (по построению), а фигура CKEG - половиной квадрата со стороной ЕК.
Найдя координату Y этой точки, получим сторону нижнего квадрата.
Решив систему уравнений (1) и (2) получим координаты точек Е(0,2;0,4) и А(1;2).
Итак, сторона нижнего квадрата ЕК = y = 0,4 ед.
Сторону FN верхнего квадрата найдем, определив координату пересечения окружности с прямой, параллельной прямой y=2x и проходящей через точку G(0;0,4) , то есть с прямой
y = 2x+0,4. После решения системы двух уравнений получим
х1 = (4,4 - 2√3,04)/5. (Второе значение нам не нужно).
Тогда y1 = x1+0,4 = (6,4 - 2√3,04)/5. =>
Cторона верхнего квадрата равна разности Y-координат точек F и E:
y1 - y = (6,4 - 2√3,04)/5 - 0,4 = (4,4 - 2√3,04)/5.
