Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить , срочно пожалуйста!!!!!!!!!!
Приложения:
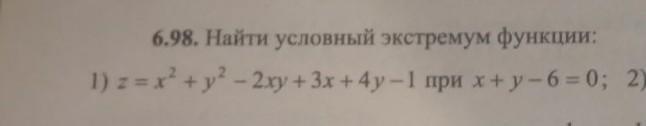
yugolovin:
4 задачи в одном задании - это плохо. Оптимально - одна задача в одном задании
Ответы
Автор ответа:
0
Поэтому функция имеет условный минимум при x=25/8; y=6-25/8=23/8.
Равен он 319/16.
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: rebeka3456
Предмет: Английский язык,
автор: tinna97
Предмет: Английский язык,
автор: EgorIsSmocking
Предмет: Русский язык,
автор: maksimtrololo62
Предмет: Математика,
автор: leosevich