Предмет: Геометрия,
автор: 9wqdjny9jq
Стороны египетского треугольника равны 3,4,5. Через центр вписанной в него окружности перпендикулярно гипотенузе провели прямую. Найдите длину отрезка этой прямой, заключённого внутри треугольника
Аноним:
r=(3+4-5)/2=1
Ответы
Автор ответа:
0
Ответ:
(ед.)
Объяснение:
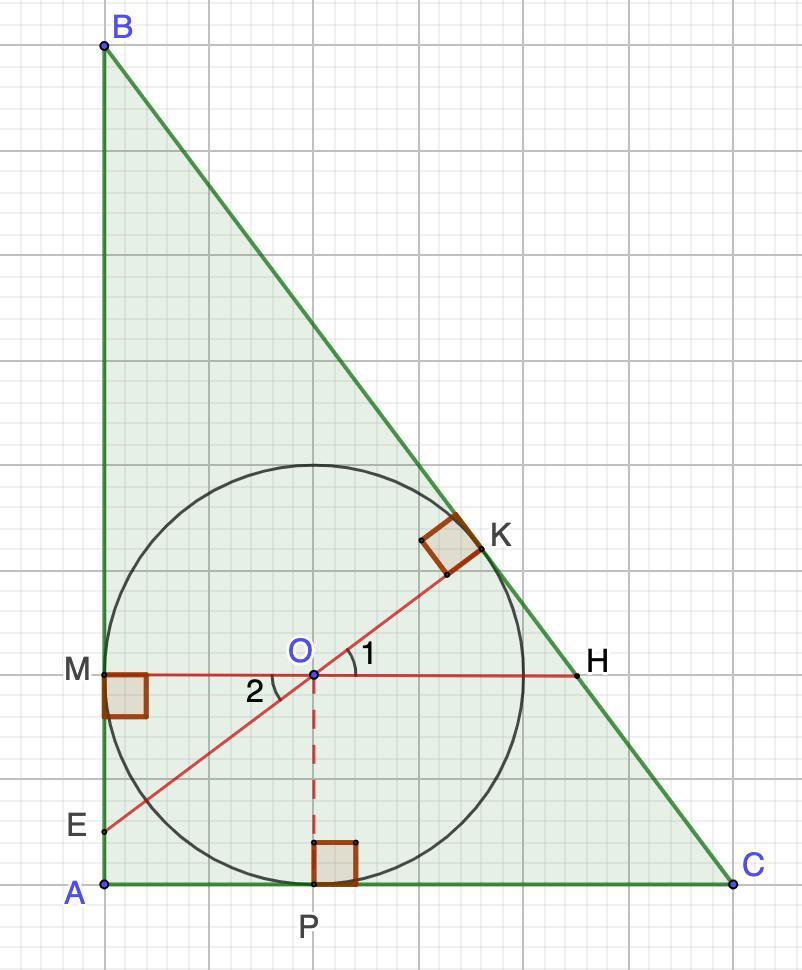
Дано: ΔАВС - прямоугольный.
АС = 3; АВ = 4; ВС = 5.
Окр. O,r - вписанная.
ЕК ⊥ ВС.
Найти: ЕК.
Решение:
1. Рассмотрим АМОР.
∠А = 90° (условие);
- Радиус, проведенный в точку касания перпендикулярен касательной.
⇒ ОР ⊥ АС; ОМ ⊥ АВ.
- Если две прямые перпендикулярны третьей, то они параллельны между собой.
⇒ АМ || АР; АР || МО.
⇒ АМОР - прямоугольник.
- Противоположные стороны прямоугольника равны.
⇒ АМ = АР; АР = МО.
МО = АР = r ⇒ АМ = АР = АР = МО.
⇒ АМОР - квадрат.
2. Найдем r по формуле:
, где a и b - катеты, с - гипотенуза.
⇒ АМ = АР = АР = МО=1
3. Рассмотрим ΔАВС и ΔМВН - прямоугольные.
∠В - общий;
⇒ ΔАВС ~ ΔМВН (по двум углам).
Составим отношение сходственных сторон:
4. Рассмотрим ΔЕМО и ΔОКН - прямоугольные.
МО = ОК = r
∠1 = ∠2 (вертикальные)
⇒ ΔЕМО = ΔОКН (по катету и острому углу)
⇒ ЕО = ОН (как соответственные элементы)
МО +ОН = ЕО + ОК = МН =
⇒
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: EgorIsSmocking
Предмет: Русский язык,
автор: Сабира11
Предмет: Русский язык,
автор: tumblrqueen
Предмет: Информатика,
автор: sakyraalena