Question

Необходимо полное решение задачи

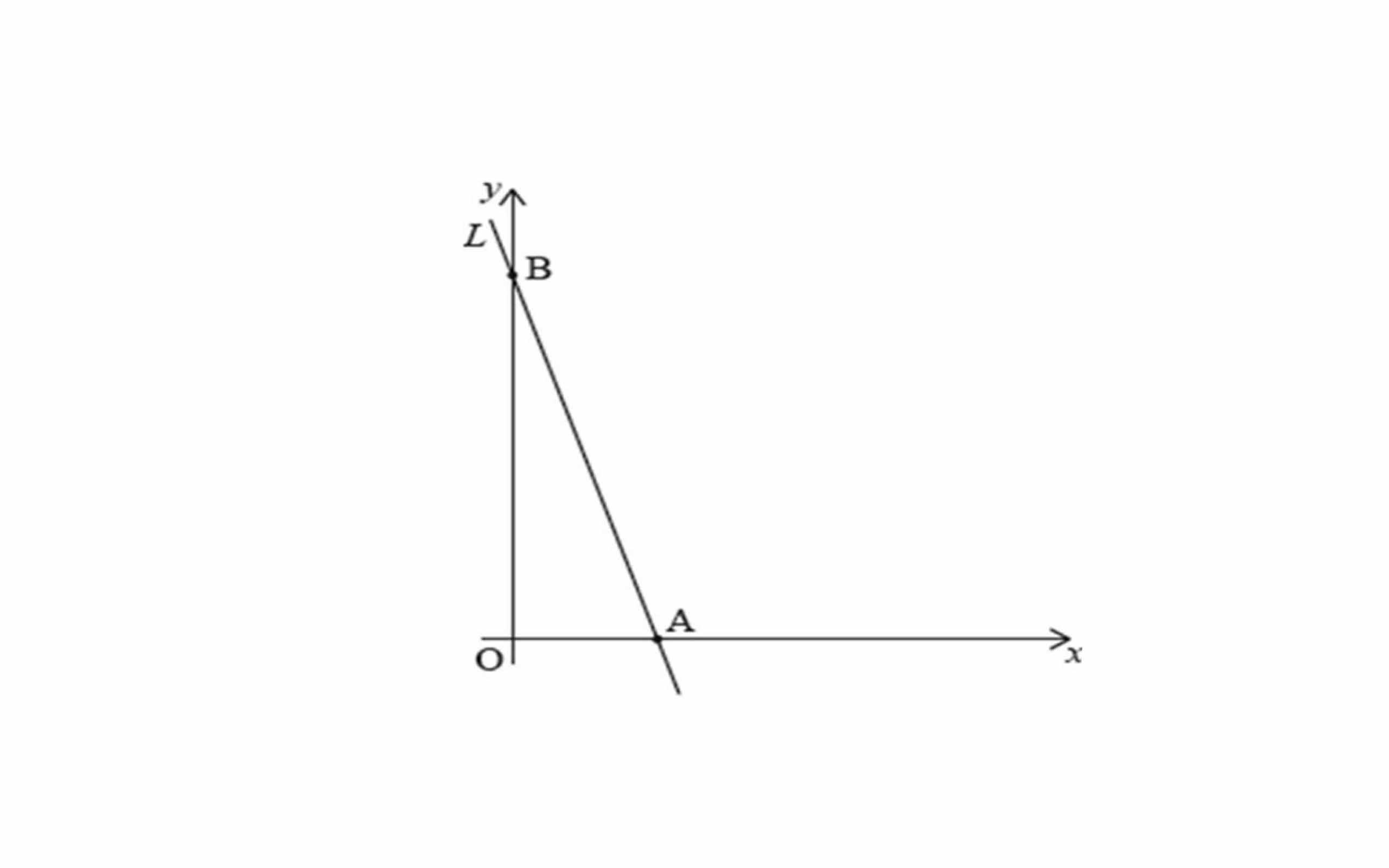
Прямая пересекает ось x в точке A и ось y в точке B, как
показано на схеме.
Точка P(2,25) находится на линии L, а длина отрезка OB в пять раз больше длины отрезка OA.

а) Найдите уравнение L в виде y = mx + c.

б) Запишите координаты точки B.

в) Найдите координаты точки A.

Answer 1

Ответ:L= -5x + 35; B(0;35); A(7;0)

Пошаговое объяснение:

Известно, что точка B лежит на Оу (х= 0), а точка А лежит на Ох (y=0). При этом длина ОВ в 5 раз больше ОА. Следовательно, частное деления этих длин даёт 5.

(1) Поскольку мы знаем, что коэффициент наклона (m) прямой есть ни что иное, как тангенс частного деления изменений по Оу и Ох, m = -5.

Здесь нужно обратить внимание на схему: убывающая прямая может быть только при негативном m.

(2) Можно найти С при помощи уравнения точки Р.

(3) (4) Координаты в этих случаях можно найти аналогично С.