Предмет: Алгебра,
автор: petrovdmitric47
СРОЧНО ПОМОГИТЕ СРОЧНО
Приложения:
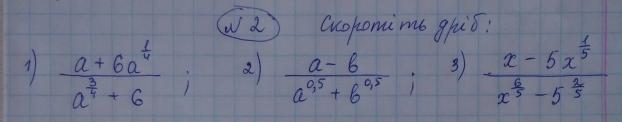
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: Kristik8
Предмет: Русский язык,
автор: fdsdsfsd
Предмет: Английский язык,
автор: uzumakinaruto07
Предмет: Биология,
автор: kingoformat