Question

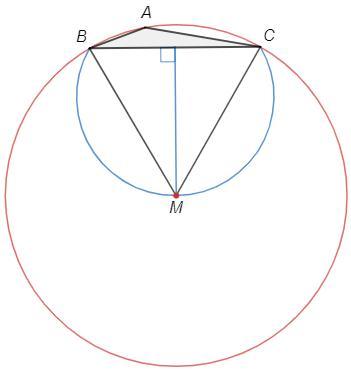
В треугольнике ABC угол В равен 20°, угол С равен 10°. Вне треугольника выбрана точка М так, что треугольник СМВ равносторонний. (Точки М и А лежат по разные стороны от прямой ВС.)

Докажите что точка М совпадает с центром описанной окружности

Answer 1

1) Центр описанной окружности лежит на серединном перпендикуляре к BC.

2) Отрезок BC виден из центра описанной окружности под углом

=∪BA+∪AC =2(∠C+∠B) =60°

ГМТ из которых отрезок виден под данным углом - две дуги. Выбираем дугу в полуплоскости, не содержащей A. Серединный перпендикуляр к BC пересекает эту дугу в единственной точке.

Точка M удовлетворяет обоим условиям, следовательно является центром описанной окружности.