Question

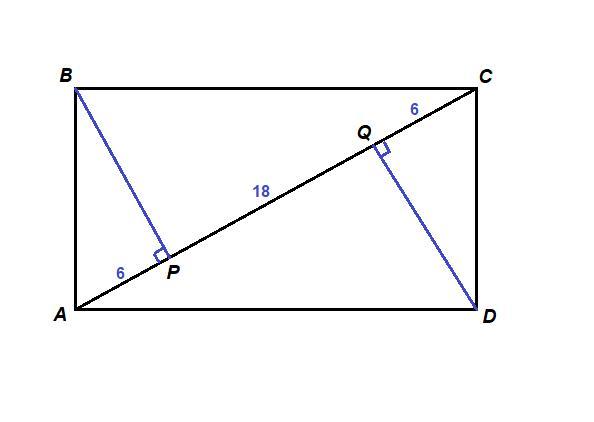
В прямоугольнике ABCD из вершин Ви D опущены перпендикуляры на диагональ АС. Эти перпендикуляры пересекают диагональ в точках РиQ соответственно. Найдите площадь прямоугольника, если AP = 6, PQ = 18. ​

Answer 1

Ответ:

360 кв. ед.

Пошаговое объяснение:

ΔABC = ΔCDA, так как диагональ делит прямоугольник на два равных треугольника, значит равны высоты, проведенные к равным сторонам:

BP = DQ.

ΔАВР = ΔCDQ по гипотенузе и катету (АВ = CD как противоположные стороны прямоугольника, ВР = DQ), значит

CQ = AP = 6.

PC = PQ + CQ = 18 + 6 = 24

AC = AP + PC = 6 + 24 = 30

ΔАВР:  ∠АРВ = 90°, ВР - его высота, тогда

  BP² = AP · PC

  BP = √(6 · 24) = √(6 · 6 · 4) = 6 · 2 = 12

$S_{ABC}=\dfrac{1}{2}AC\cdot BP=\dfrac{1}{2}\cdot 30\cdot 12=\dfrac{1}{2}\cdot 360$

Площадь прямоугольника в 2 раза больше:

$S=2S_{ABC}=360$