Предмет: Алгебра,
автор: petrovdmitric47
Спростіть вираз. СРОЧНО ПОМОГИТЕ
Приложения:
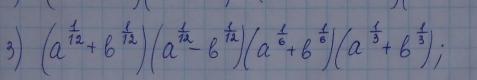
Ответы
Автор ответа:
1
Ответ:
Объяснение:
petrovdmitric47:
СПАСИБО
привет, можешь и мое решить??
Похожие вопросы
Предмет: Русский язык,
автор: saika00
Предмет: Английский язык,
автор: OLOLOLOSH
Предмет: Русский язык,
автор: akmaralkamila
Предмет: Алгебра,
автор: maavean