Предмет: Алгебра,
автор: anyanajdenova69
СРОЧНО, НУЖНА ПОМОЩЬ!
Приложения:
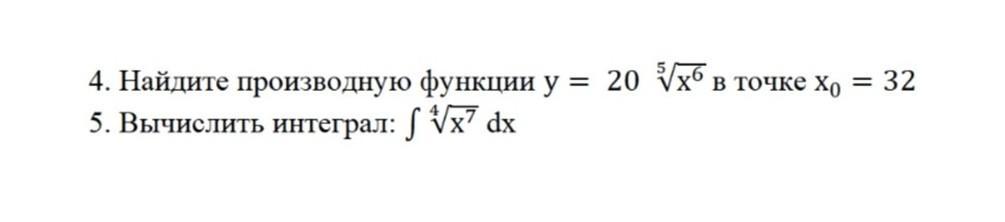
Ответы
Автор ответа:
1
Ответ:
Объяснение:
4.
Поскольку (c*f(x))' = c*f(x)', то полученную производную, домножим затем на 20.
Поскольку:
домножаем на 20
поставляем точку х₀
получаем
5.
Это табличный интеграл
anyanajdenova69:
огромное спасибо тебе ❤️
Похожие вопросы
Предмет: Английский язык,
автор: 1qqqqqee
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Termenahter
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: GreatNut