Предмет: Алгебра,
автор: idoxxoxo
помогите пожалуйста!!!
Приложения:
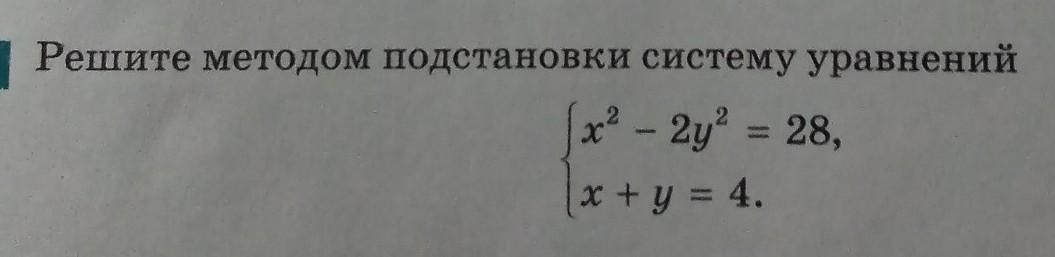
Ответы
Автор ответа:
0
Ответ:вот
Объяснение:
Приложения:

Автор ответа:
0
Ответ:
ситема уравнений имеет две пары решений
(6;-2) ; (10;-6)
Решение:
теперь решаем первое уравнение( из системы)
-у²-8у-12=0
Найдём дискриминант
D=64-4*(-1)*(-12)=64-48=16
теперь найдём корни
первая пара решения системы (6; -2)
вторая пара решения системы (10;-6)
Похожие вопросы
Предмет: Английский язык,
автор: K0L
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: ЕленаЛаврова2016
Предмет: Математика,
автор: gimpro00
Предмет: Литература,
автор: Аноним