Предмет: Математика,
автор: Аняff
помогите пожалуйста.
Приложения:
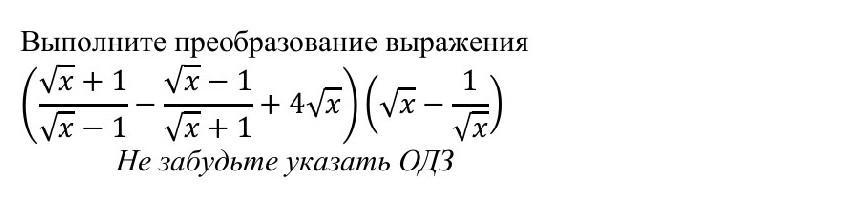
pelmeshkavsmetani:
если помогут то скажите
помогли
спс
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Решение: ОДЗ: (Мы получили это так как подкоренное должно быть больше или равно нулю т.е.
и знаменатели не равны нулю т.е.
и
и
, самое последнее верно при всех икс)
Преобразования:
Похожие вопросы
Предмет: Русский язык,
автор: Worsethanhell
Предмет: Русский язык,
автор: Smashing7
Предмет: Русский язык,
автор: Karjal
Предмет: Математика,
автор: rmnvktr
Предмет: География,
автор: 1233153