Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить , срочно
Приложения:
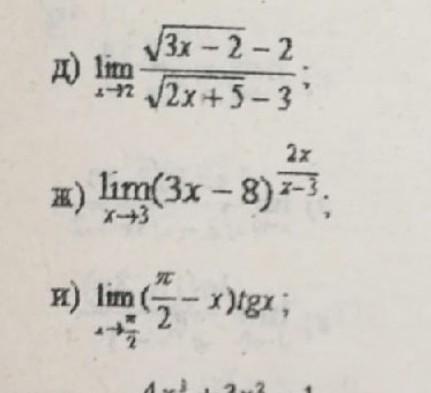
Ответы
Автор ответа:
1
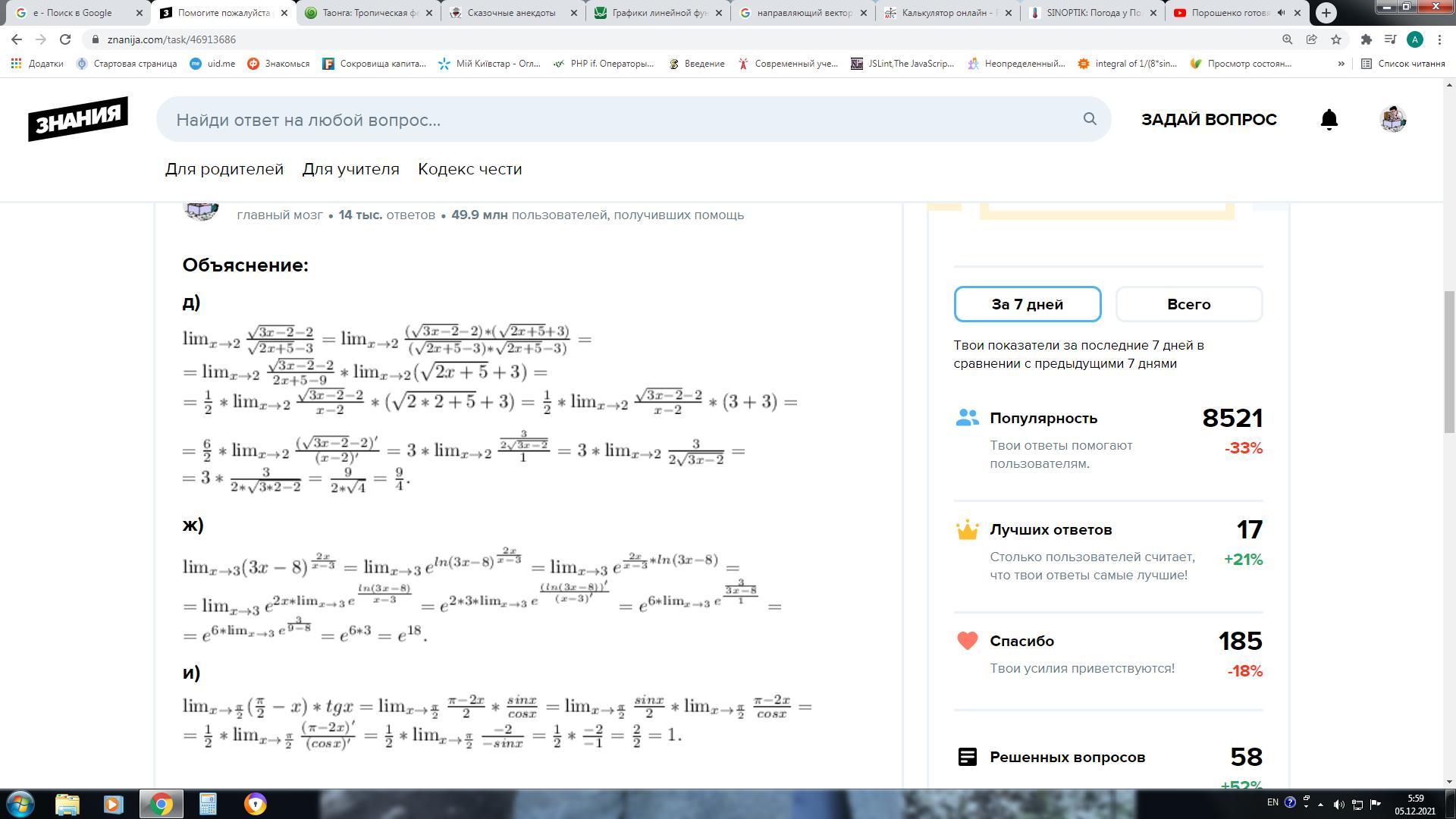
Объяснение:
д)
ж)
и)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: макс239
Предмет: Английский язык,
автор: Rainbow161
Предмет: Английский язык,
автор: Alinaaa12345
Предмет: Английский язык,
автор: Lisateo04
Предмет: Литература,
автор: YuliaMaryKay