Предмет: Алгебра,
автор: alexxxandrova
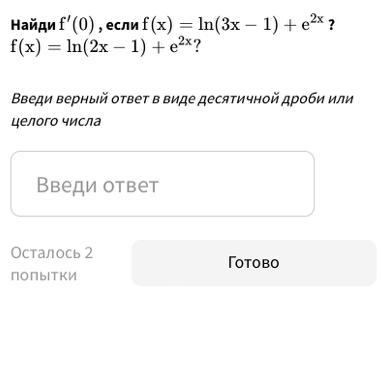
Найди f'(0) , если f (x) = ln(3х – 1) + e^2x ?
f(x) = ln(2x – 1) + е^2х?
Приложения:
Ответы
Автор ответа:
0
Ответ:
-1
0
Объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: ngroza64
Предмет: Русский язык,
автор: msdybkova
Предмет: Русский язык,
автор: VIPPasha
Предмет: Литература,
автор: enotishka05