Предмет: Алгебра,
автор: maxvah
Решите пожалуйста 2 системы...

Приложения:
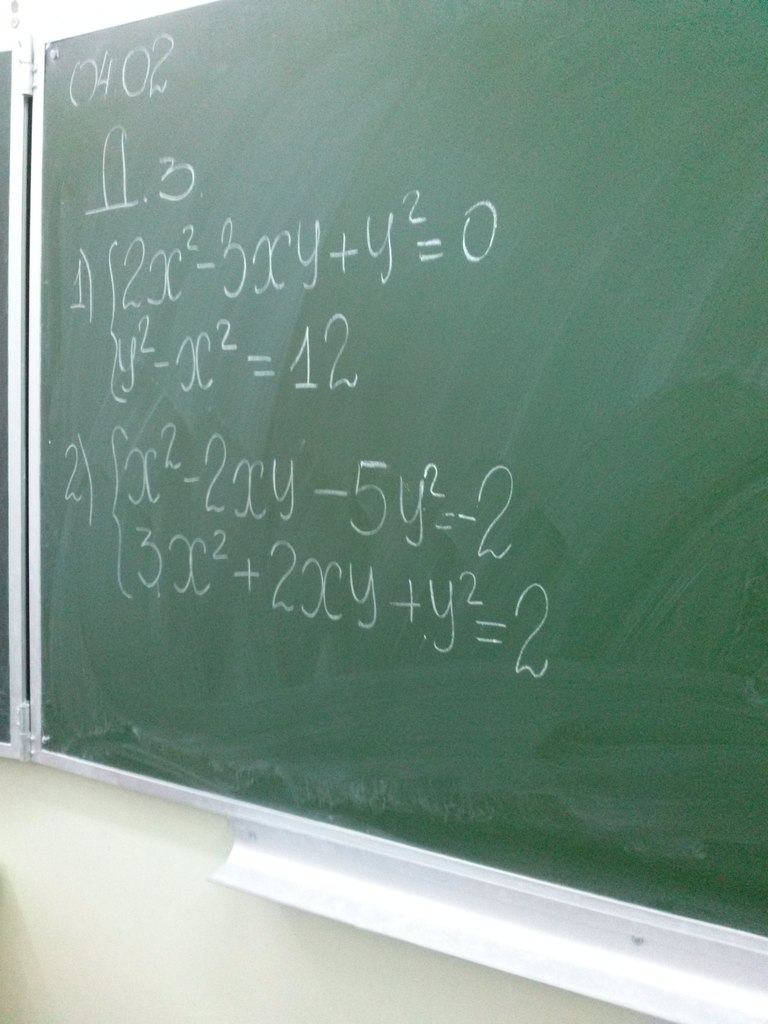
Ответы
Автор ответа:
0
1) решим первое уравнение как квадратное относительно х.
2x^2 - 3y*x + y^2 = 0
D=(-3y)^2 - 4*2*y^2 = y^2
x1 = (3y + |y|)/4
x2 = (3y - |y|)/4
Подставляем каждое х во второе уравнение и ищем корни:
y^2 - (9y^2 + 6y^2 + y^2)/16 = 12
16y^2 - 16y^2 = 12*16 - не верно, значит х1 не является корнем.
y^2 - (9y^2 - 6y^2 + y^2)/16 = 12
16y^2 - 4y^2 = 12*16
12y^2 = 12*16, y^2 = 16
y = +-4 - значит х2 является корнем, найдем его:
y = 4, x = (3*4 - 4)/4 = 2
y = -4, x = (-12 - 4)/4 = -4
Ответ: (2;4), (-4;-4)
2) сложим оба уравнения, получим:
4x^2 - 4y^2 = 0
(x - y)(x + y) = 0
x=y, x= -y
x=y, y^2 - 2y^2 - 5y^2 = -2, -6y^2 = -2, y^2 = 1/3, y = +-√3/3
x= -y, y^2 + 2y^2 - 5y^2 = -2, -2y^2 = -2, y^2 = 1, y = +-1
Ответ: (-√3/3; -√3/3), (√3/3; √3/3); (-1;1), (1;-1)
2x^2 - 3y*x + y^2 = 0
D=(-3y)^2 - 4*2*y^2 = y^2
x1 = (3y + |y|)/4
x2 = (3y - |y|)/4
Подставляем каждое х во второе уравнение и ищем корни:
y^2 - (9y^2 + 6y^2 + y^2)/16 = 12
16y^2 - 16y^2 = 12*16 - не верно, значит х1 не является корнем.
y^2 - (9y^2 - 6y^2 + y^2)/16 = 12
16y^2 - 4y^2 = 12*16
12y^2 = 12*16, y^2 = 16
y = +-4 - значит х2 является корнем, найдем его:
y = 4, x = (3*4 - 4)/4 = 2
y = -4, x = (-12 - 4)/4 = -4
Ответ: (2;4), (-4;-4)
2) сложим оба уравнения, получим:
4x^2 - 4y^2 = 0
(x - y)(x + y) = 0
x=y, x= -y
x=y, y^2 - 2y^2 - 5y^2 = -2, -6y^2 = -2, y^2 = 1/3, y = +-√3/3
x= -y, y^2 + 2y^2 - 5y^2 = -2, -2y^2 = -2, y^2 = 1, y = +-1
Ответ: (-√3/3; -√3/3), (√3/3; √3/3); (-1;1), (1;-1)
Автор ответа:
0
1) из 1 ур-ия системы вычтем 2 и получим:
 (*)
(*)
из 2 ур-ия системы:

подставим в (*) вместо -12 выражение (x-y)(x+y)
получим:
3x(x-y)=(x-y)(x+y) и разделим на (x-y)≠0
3x=x+y
2x=y подставим во 2 ур-ие системы и получим:


2) Сложим 1 и 2 ур-ия системы и получим:

Либо x=y
либо x=-y
Рассмотрим x=y.
Подставим в 1 ур-ие системы:
y²-2y²-5y²=-2
-6y²=-2


Рассмотрим x=-y.
Подставим в 1 ур-ие системы:
y²+2y²-5y²=-2
-2y²=-2
y²=1

из 2 ур-ия системы:
подставим в (*) вместо -12 выражение (x-y)(x+y)
получим:
3x(x-y)=(x-y)(x+y) и разделим на (x-y)≠0
3x=x+y
2x=y подставим во 2 ур-ие системы и получим:
2) Сложим 1 и 2 ур-ия системы и получим:
Либо x=y
либо x=-y
Рассмотрим x=y.
Подставим в 1 ур-ие системы:
y²-2y²-5y²=-2
-6y²=-2
Рассмотрим x=-y.
Подставим в 1 ур-ие системы:
y²+2y²-5y²=-2
-2y²=-2
y²=1
Похожие вопросы
Предмет: Русский язык,
автор: lagieto50
Предмет: Математика,
автор: drakass961
Предмет: Литература,
автор: babichenko170382
Предмет: Литература,
автор: Алиса50