Question

около шара радиуса R описан правильный конус. Найдите площадь поверхности конуса.

Answer 1

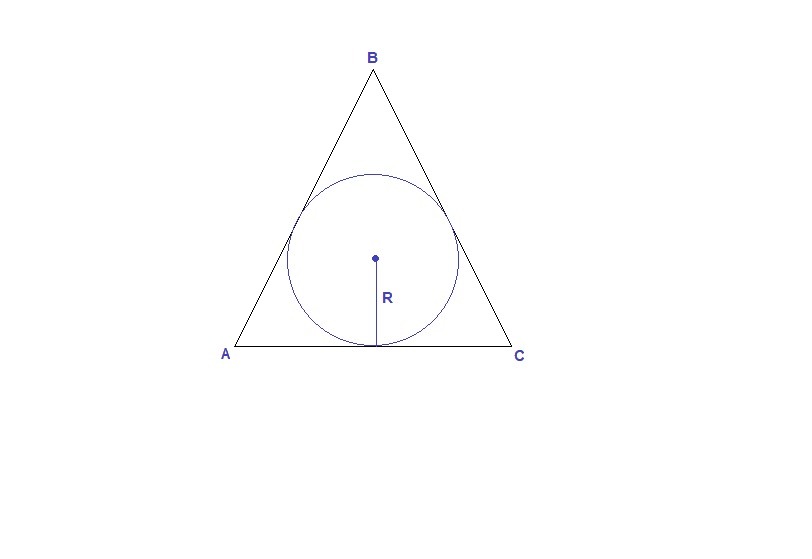
Осевое сечение конуса - равносторонний треугольник.  Сечение шара, проходящее через его центр, круг, - вписанный в равносторонний треугольник.

Радиус круга, вписанного в правильный треугольник:

R = a√3/6, где а - сторона треугольника, тогда

a = 6R / √3 = 2R√3

Радиус основания конуса равен половине стороны треугольника, образующая - стороне:

r = a/2 = R√3,

l = a = 2R√3.

Sпов. = πrl + πr² = πr(l + r) = πR√3 (2R√3 + R√3)  =

= πR√3 · 3R√3 = 9πR²