Question

Срочно даю 50 балов!!!!!
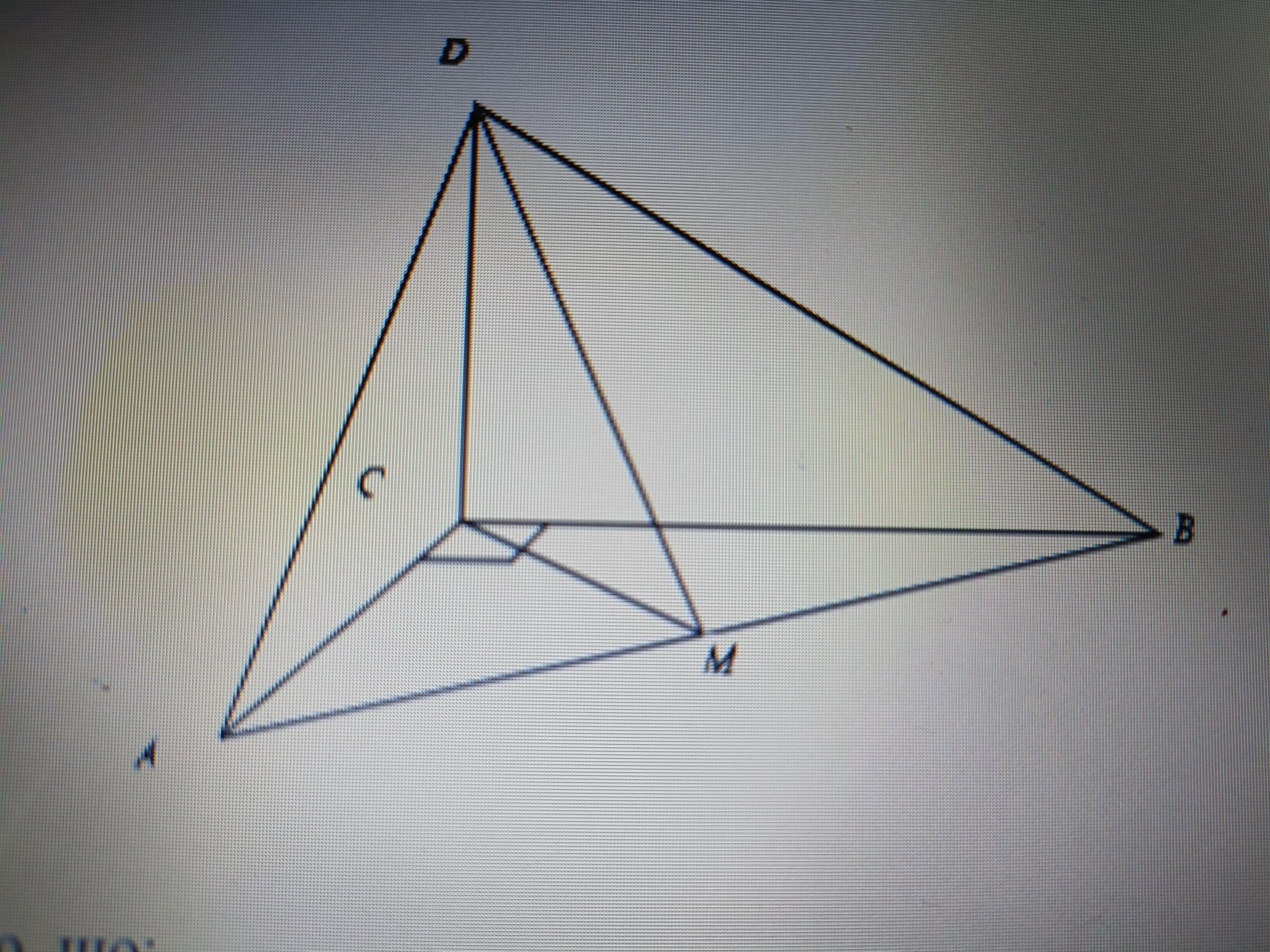
С вершины прямого угла c треугольника ABC проведен перпендикуляр

CD к плоскости треугольника. DB и DA - наклонные.

DC= 1см;

CА= 4см;

DB= корень10 см.

Найти:

1. длину неизвестной наклонной;

2. длину неизвестной проекции;

3. длину отрезка АВ;

4. Длина медианы CM;

5. длина отрезка DM;

6. расстояние от точки В до плоскости DCM.

Answer 1

Ответ:

Объяснение: (V -корень,  ^ -знак степени,  3^2 -это 3 в квадрате)

находим все по теор. Пифагора

1) тр. ADC   AD=V(4^2 +1^2)=V(17)

2) тр. DBC  CB=V((V10)^2 - 1^2))=V9=3

3) тр. ACB  AB=V(4^2+3^2)=V(16+9)=5

4) Медиана, проведенная к гипотенузе равна 1/2 гипотенузы,  CM=1/2 AB,

CM=5/2

5)  тр. DCM   DM=V(1^2 +(5/2)^2)=V(29/4)=V(29) /2

6) проведем  BK перпендикулярно  МС   и  BK  перпендикулярна  DC, значит  BK перпендикулярна плоскости DCM, значит,  BK  есть расстояние от точки  B  до плоскости DCM. Надо найти BK/

S(ABC)=1/2 AC*CB=1/2*4*3=6,   тогда  S(MCB)=6/2=3 и  S(MCB)=1/2*MC*BK,

3=1/2*5/2 *BK,   12=5BK,  BK=12/5=2,4    ,  расстояние =2,4