Предмет: Математика,
автор: uxaisha586
50 баллов!!!
Нужно найти производную функции.
Любые два примеры
Приложения:
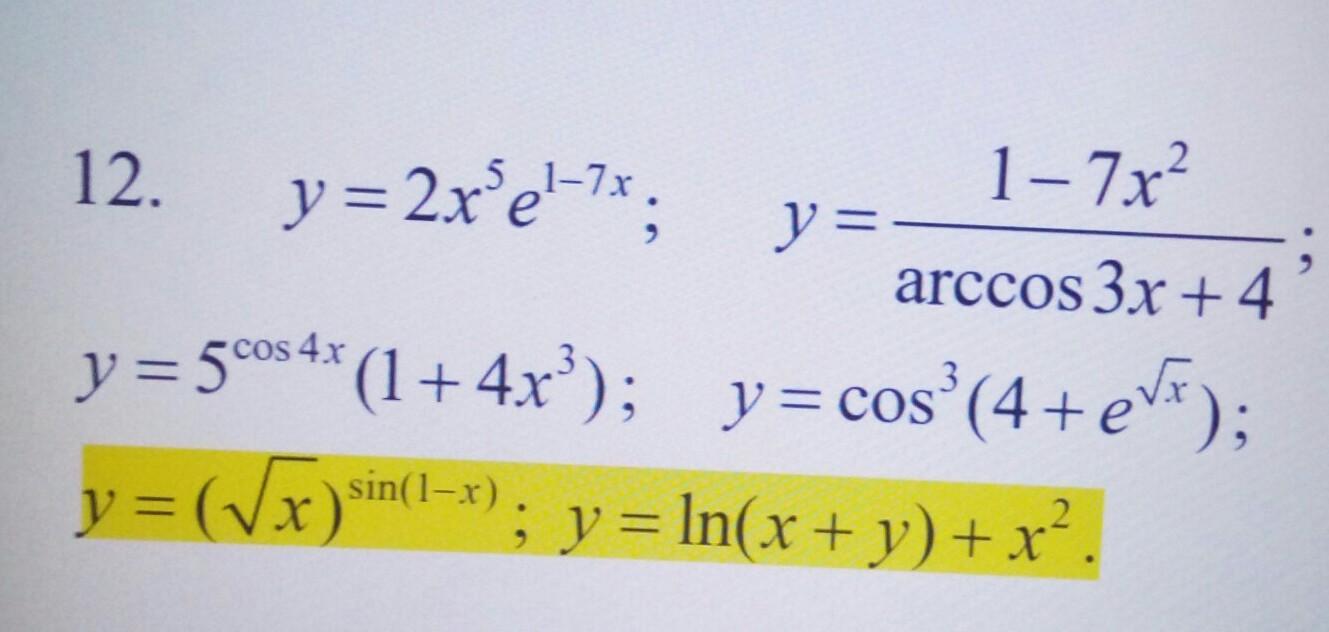
Ответы
Автор ответа:
1
Ответ: ,
Пошаговое объяснение:
uxaisha586:
спасибо
Похожие вопросы
Предмет: Другие предметы,
автор: yapirog96
Предмет: Русский язык,
автор: HennesseyN1
Предмет: Русский язык,
автор: Аноним
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Информатика,
автор: khramovtima