решите неравенства Алгебра
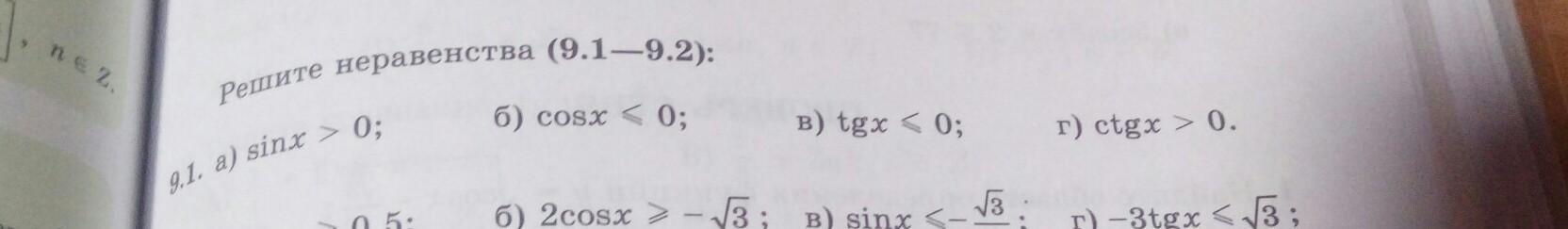
Ответы
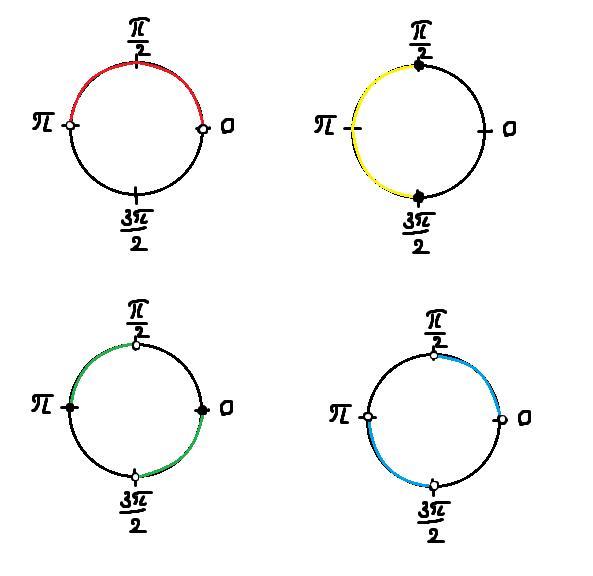
// Воспользуемся тригонометрической единичной окружностью (во вложении)
sin x > 0 (красный) - в верхней половине, а значит x ∈ (0 ; π).
Поскольку мы не ограничиваемся одним оборотом по окружности, а синус является периодической функцией с T = 2π, ответом для всего промежутка будет x∈(2πk ; π + 2πk), k ∈ Z.
cos x ≤ 0 (жёлтый) - в левой половине, а значит x ∈ (π/2 ; 3π/2).
Поскольку мы не ограничиваемся одним оборотом по окружности, а косинус является периодической функцией с T = 2π, ответом для всего промежутка будет x∈(π/2 + 2πk ; 3π/2 + 2πk), k ∈ Z.
tg x ≤ 0 (зелёный) - во второй и четвёртой четвертях, а значит x ∈ (π/2 ; π] ∪ (3π/2 ; 2π].
Поскольку мы не ограничиваемся одним оборотом по окружности, а тангенс является периодической функцией с T = π, ответом для всего промежутка будет x ∈ (π/2 + πk ; π + πk].
ctg x > 0 (голубой) - в первой и третьей четвертях, а значит x ∈ (0 ; π/2) ∪ (π ; 3π/2).
Поскольку мы не ограничиваемся одним оборотом по окружности, а котангенс является периодической функцией с T = π, ответом для всего промежутка будет x ∈ (πk ; π/2 + πk).