Предмет: Геометрия,
автор: karssad
Решите пожалуйста, срооочно
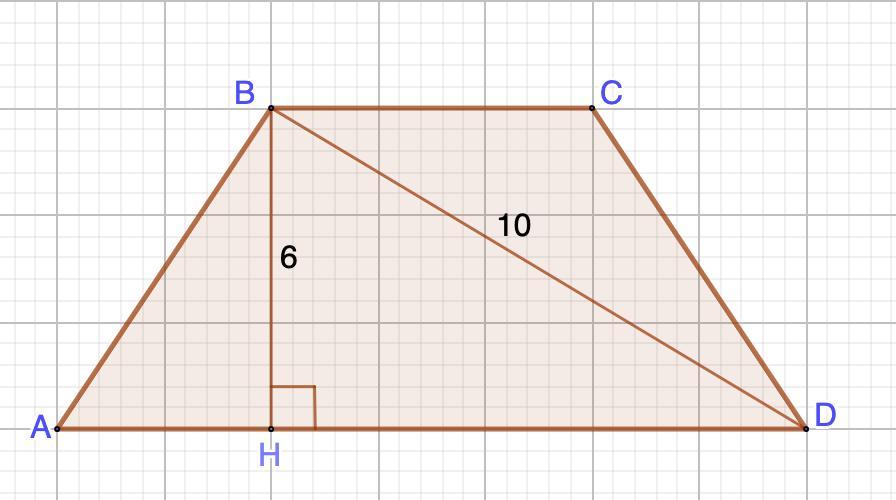
В равнобедреенной трапеции диагональ равна 10см , а высота 6см. найдите площадь трапеции
Ответы
Автор ответа:
1
Ответ:
48 см²
Объяснение:
Дано: ABCD - равнобедренная трапеция.
BD = 10 см - диагональ;
ВН = 6 см - высота
Найти: S трапеции
Решение:
Рассмотрим ΔHBD - прямоугольный.
По теореме Пифагора:
HD² = BD² - BH²
HD² = 100 - 36 = 64
HD = √64 = 8 (см)
- Свойство равнобедренной трапеции: Высота, опущенная из вершины тупого угла к большему основанию, делит его на части, большая из которых равна полусумме оснований.
⇒
Найдем площадь трапеции:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: nataliyakichigi
Предмет: Русский язык,
автор: масяня138
Предмет: Русский язык,
автор: VadimTurturika
Предмет: Химия,
автор: radislava56
Предмет: Русский язык,
автор: Tiifu