Предмет: Алгебра,
автор: dariacerska
Помогите, пожалуйста, с четвёртым
Приложения:
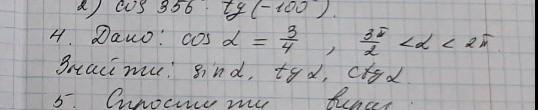
Ответы
Автор ответа:
0
Объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: sbakhtina2016
Предмет: Окружающий мир,
автор: ekvrt2005
Предмет: Русский язык,
автор: 6667774858
Предмет: Биология,
автор: vladashinkarenko2051
Предмет: Математика,
автор: flexerinterneta