Предмет: Алгебра,
автор: mironovanv1234
Алгебра 11,клас будь ласка))))
Приложения:
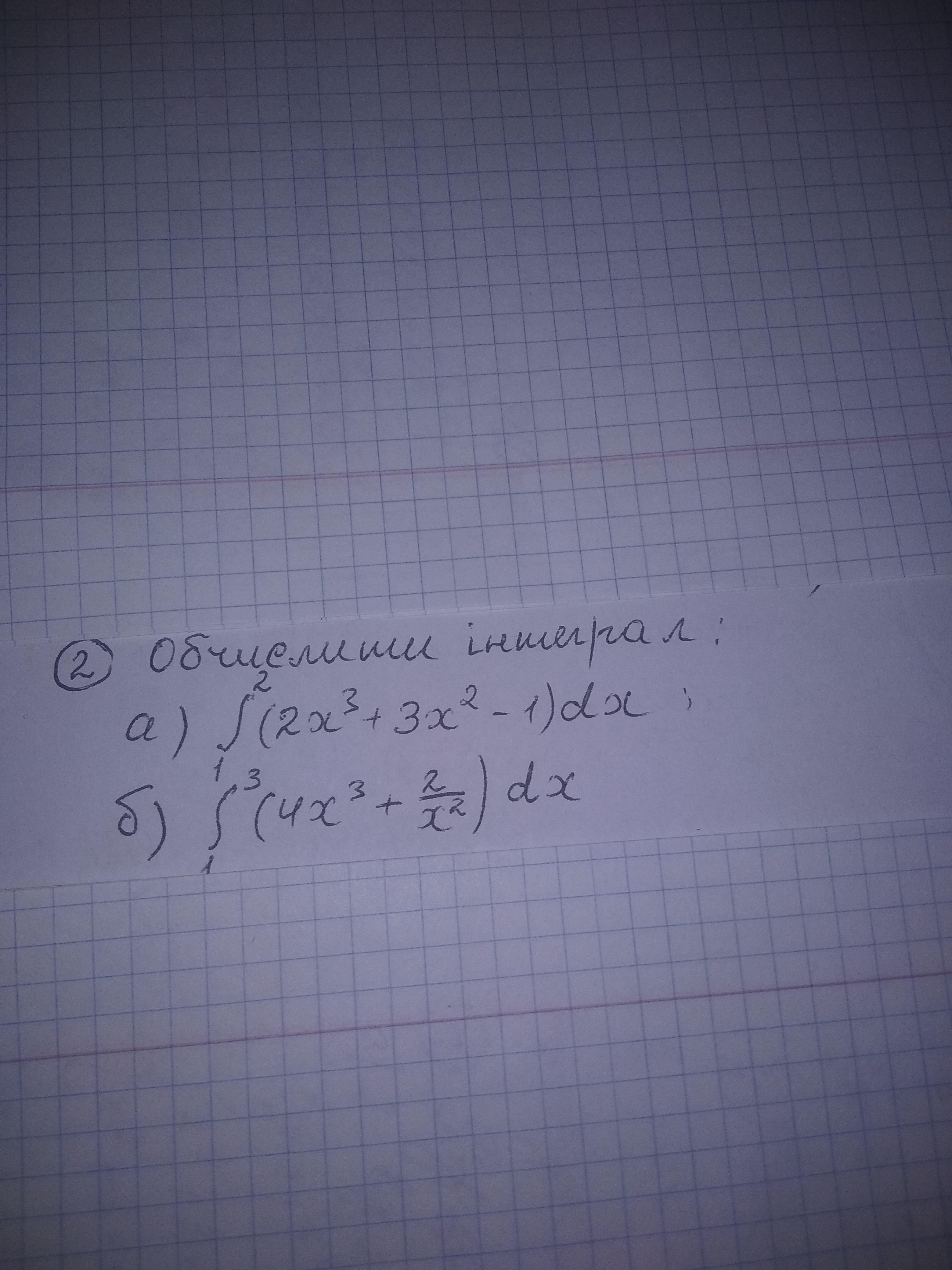
Ответы
Автор ответа:
1
Ответ:
Рішення на фото
Объяснение:
Приложения:
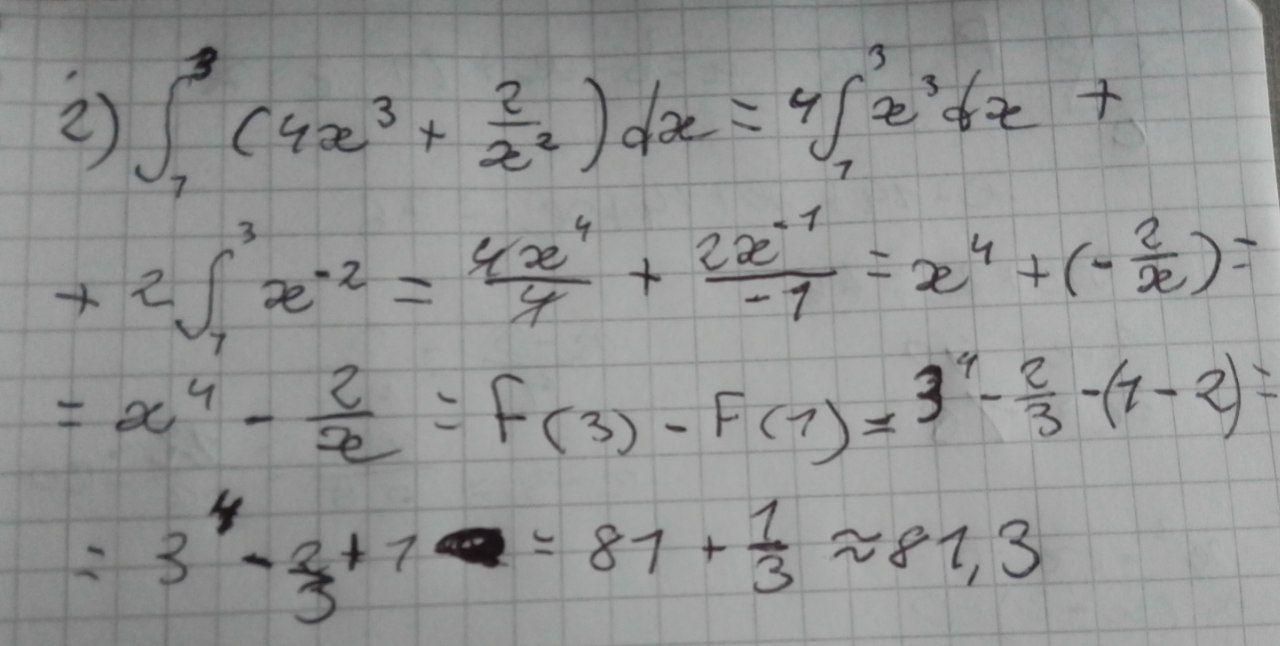
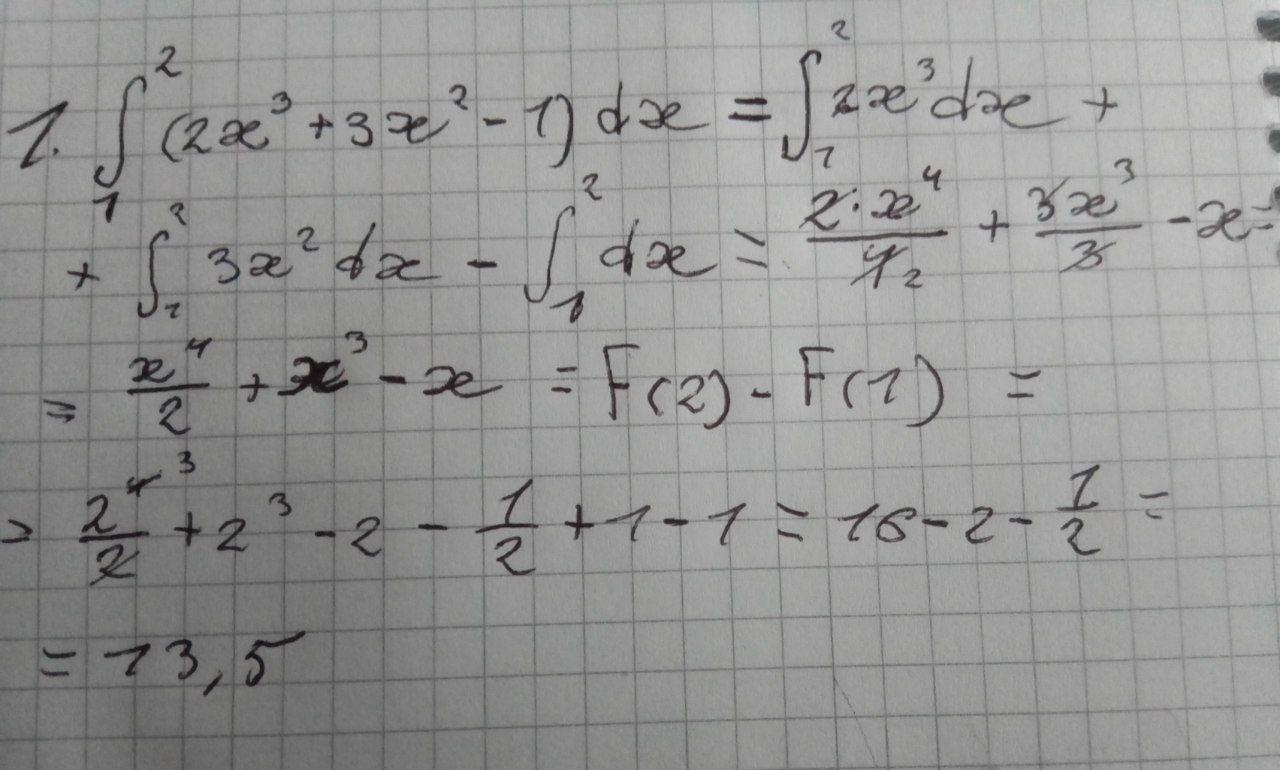
Автор ответа:
0
Объяснение:
2.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: nastyamaksmuk
Предмет: Английский язык,
автор: Эдера1
Предмет: Русский язык,
автор: lkarimova95485
Предмет: Литература,
автор: mihailovna21
Предмет: Музыка,
автор: emilsalimov