Предмет: Алгебра,
автор: pastushok2004
Ліміти
100 балів!!!!
Приложения:
Ответы
Автор ответа:
0
Ранения на фото. на втором фото будет второй вариант решения последнего примера.
Приложения:


Автор ответа:
0
Объяснение:
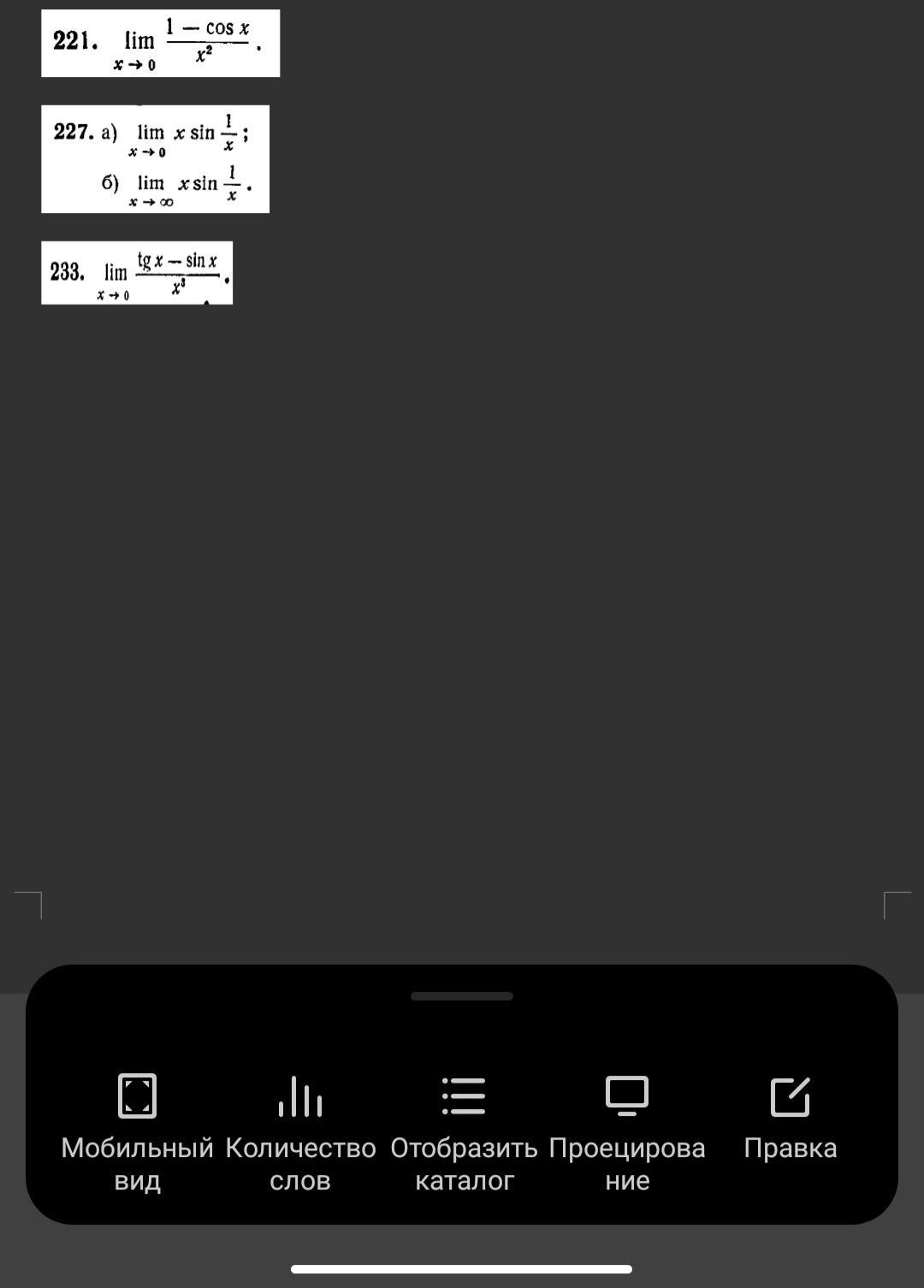
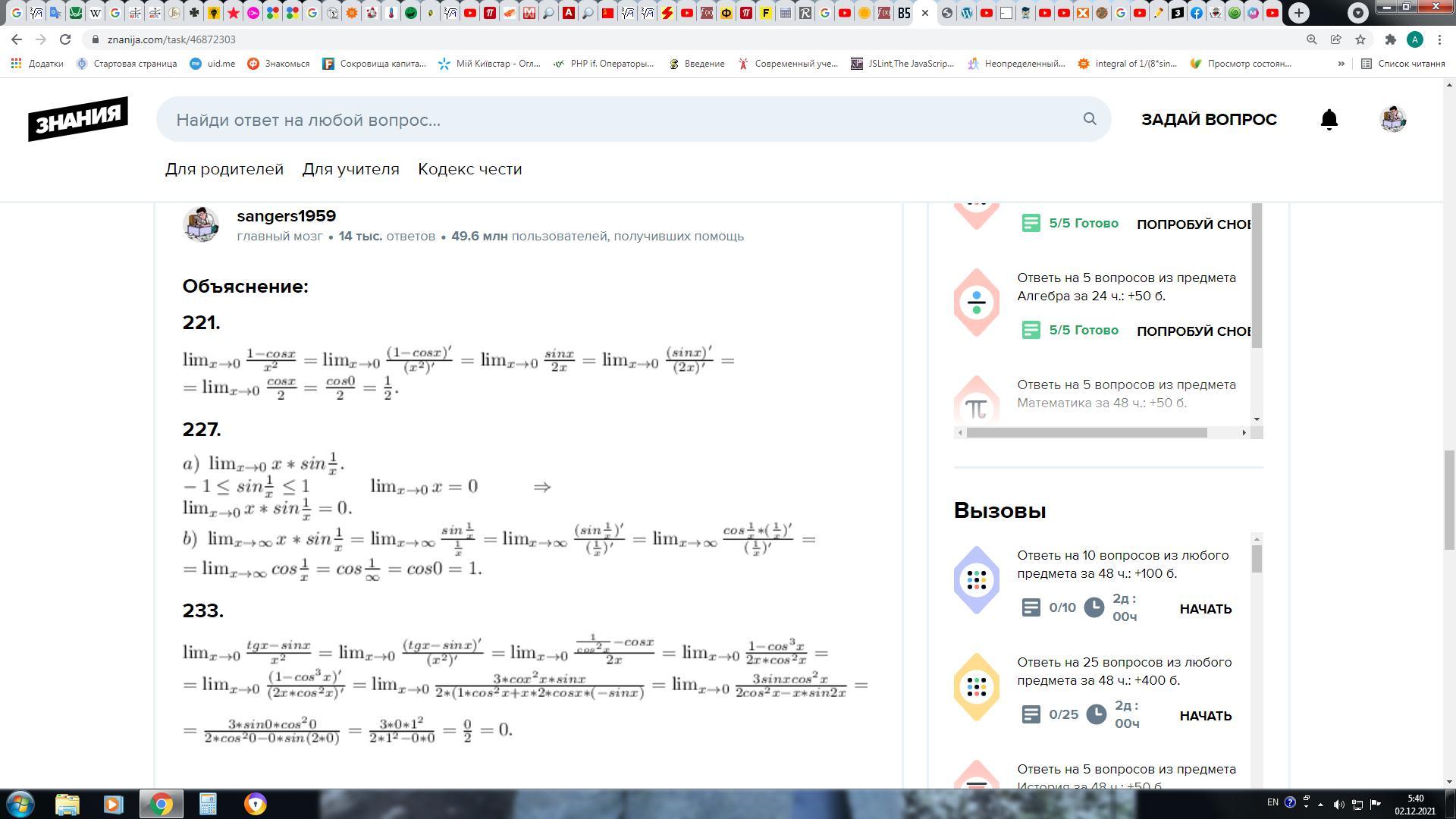
221.
227.
233.
Приложения:
IdleFri:
там вроде в последнем примере, в знаменателе х³
Похожие вопросы
Предмет: Русский язык,
автор: dolly27
Предмет: Українська література,
автор: kibaloolya
Предмет: Окружающий мир,
автор: мафия35
Предмет: Другие предметы,
автор: валерия923
Предмет: Математика,
автор: anelya2146