Предмет: Алгебра,
автор: melldsw
Помогите пожалуйста, нужно подробное решение.
Приложения:
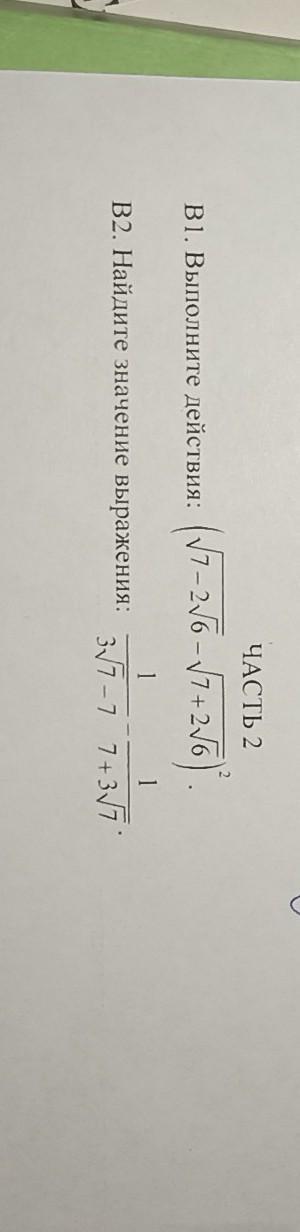
Ответы
Автор ответа:
1
Ответ:
Объяснение:
1.
Возведем в квадрат по формуле:
Также вспомним:
Получим
2.
Приведем к общему знаменателю и упростим:
melldsw:
Спасибо большое! Всё очень понятно и доступно ☺️
)))
Похожие вопросы
Предмет: Русский язык,
автор: ьчтвв
Предмет: Русский язык,
автор: mashaM13
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: maributenko03mailru
Предмет: Английский язык,
автор: Аноним