Question

Треугольник KLM вписан в окружность, OK = 16,5 м.

157 Окружность.png

Вычисли:

∢ LKM=
°;

∪ML=
°;

ML=
м.

Answer 1

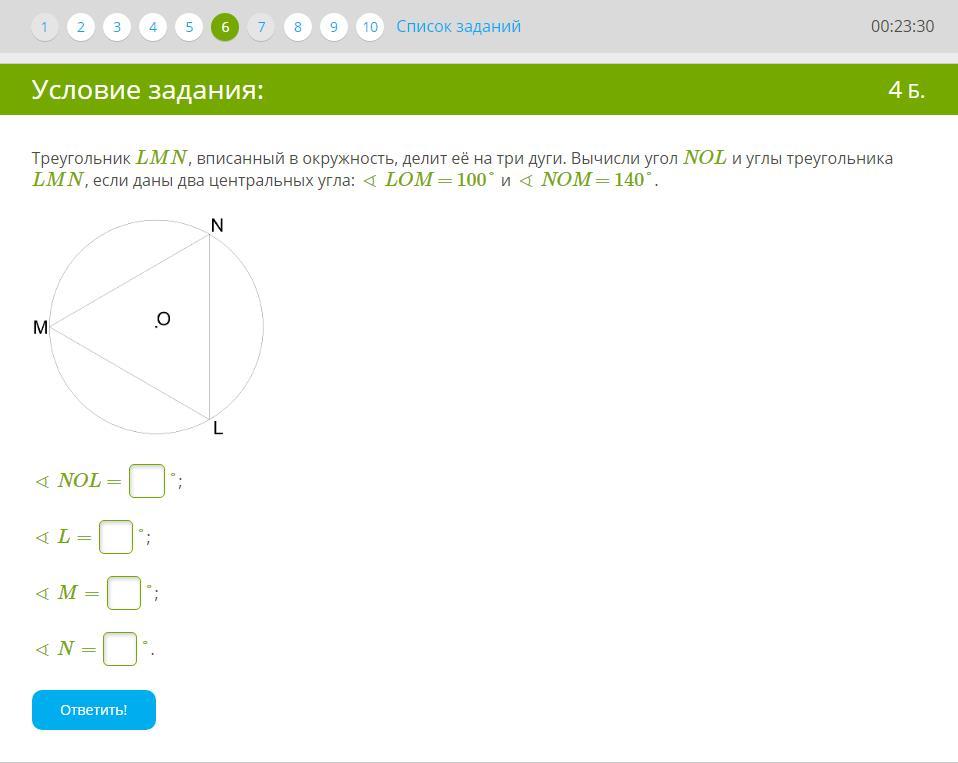
Ответ: ∠NOL=120°, ∠L=70°, ∠М=60°, ∠N=50°

Объяснение:

1) ∠NOL + ∠LOM + ∠NOM = 360° (т.к. окружность)

∠NOL + 100° + 140° = 360°

∠NOL = 360° -  (100° + 140°) = 120°

2) ∠N =  ∠MON + ∠ONL

∠M = ∠NMO + ∠LMO

∠L = ∠MLO + ∠NLO

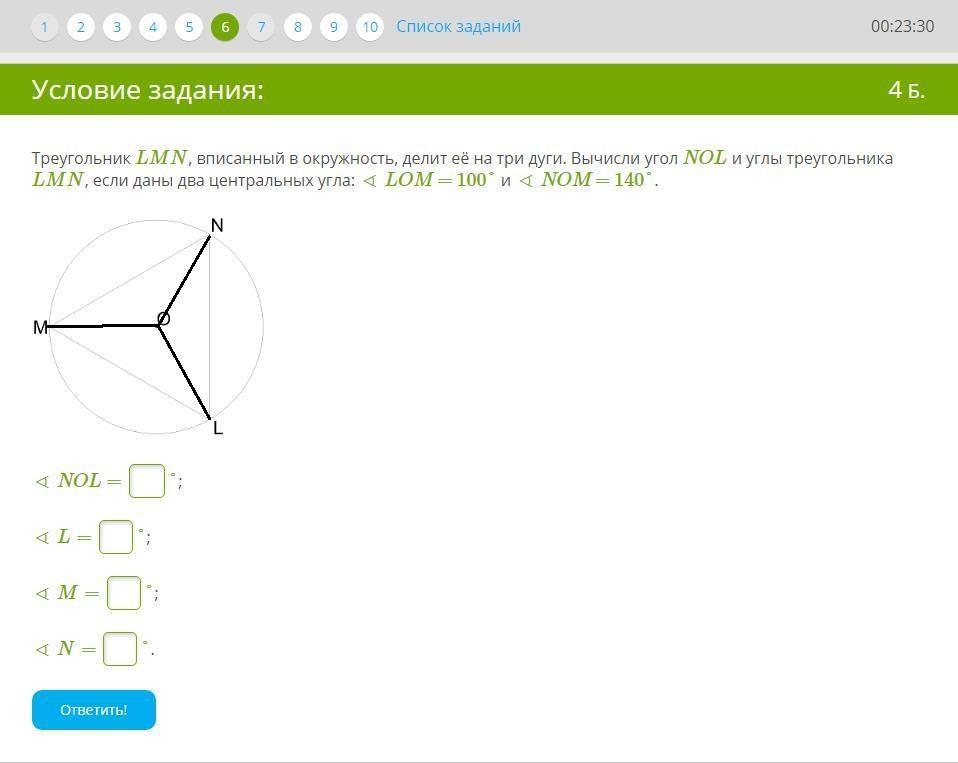
3) Рассмотрим треугольник MON:

MO = ON (т.к. радиусы) ⇒

треугольник MON - равнобедренный ⇒

∠MNO = ∠OMN

∠MON + ∠MNO + ∠OMN = 180° (по сумме углов треугольника)

140° + ∠MNO + ∠MNO = 180°

2×∠MNO = 180° - 140°

∠MNO = 40° / 2 = 20°

∠MNO = ∠OMN = 20°

Аналогично находим углы ONL(30°), OLN(30°), OLM(40°), OML(40°)

4) из п. 2 и п. 3 имеем:

∠N =  ∠MNО + ∠ONL = 20° + 30° = 50°

∠M = ∠NMO + ∠LMO = 20° + 40° = 60°

∠L = ∠MLO + ∠NLO = 40° + 30° = 70°