Предмет: Математика,
автор: zpdsl
Дан квадрат с секущей 6 см, найти периметр и площадь
Приложения:
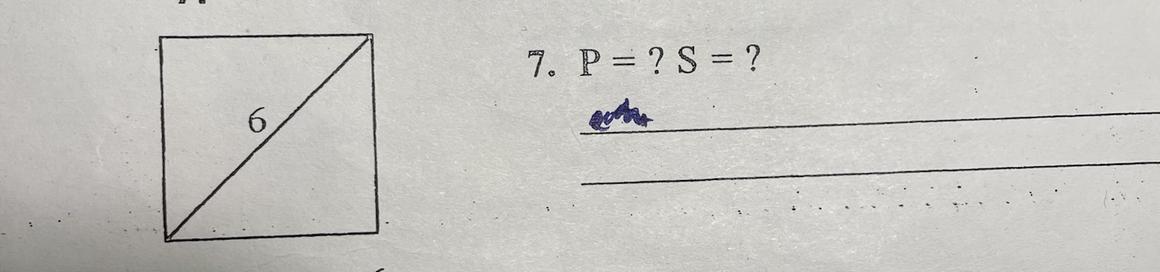
mathgenius:
секущая? Может диагональ? S = d^2/2 = 6*6/2 = 18; P = 4*6/√2 = 24/√2 = 24√2/2 = 12√2
Ответы
Автор ответа:
1
Ответ:
Диагонали квадрата равны. Площадь квадрата можно найти как половину произведения его диагоналей:
По теореме Пифагора находим длину стороны квадрата:
Так как диагональ = 6 см, то
Находим периметр квадрата:
Приложения:

Можете пожалуйста скинуть вторую строчку, она растянулась и ничего не понятно
приложила скрин
Спасибо большое
Похожие вопросы
Предмет: Русский язык,
автор: alaaaaaaa
Предмет: Русский язык,
автор: lysovaalenka
Предмет: Окружающий мир,
автор: анна697
Предмет: Русский язык,
автор: KatyaStd
Предмет: Геометрия,
автор: Аноним