Предмет: Алгебра, автор: Fimus

СРОЧНО решите неравенство
$6^{x} +6^{x+2}\leq 222$

$5^{2x}$ меньше $3^{x}$
$7^{x+1} -7^{x} \geq 294$

Ответы

Автор ответа: drtsv

Решение представлено на фото

Приложения:

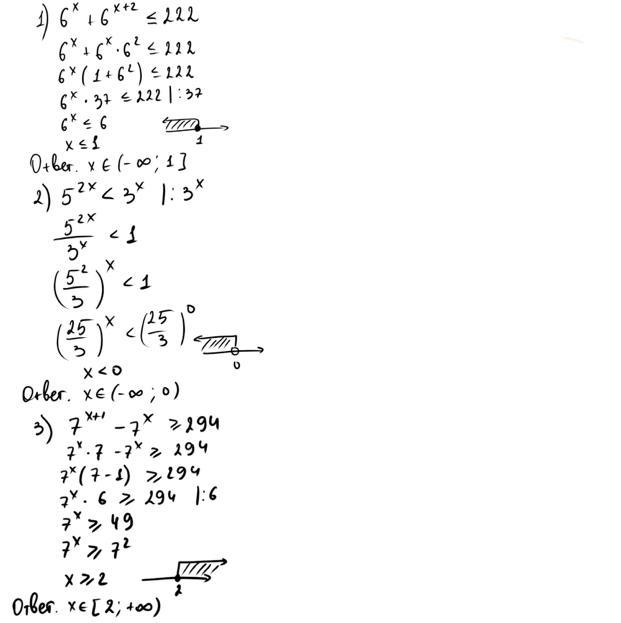
Fimus: Спасибо вам большое!

drtsv: Рада была помочь☺️

Fimus: Извините, а можете пожулйста объяснить как находить ОДЗ?

drtsv: ОДЗ находится для тех уравнений или неравенств, в которых присутствуют корень, деление на переменную или логарифм.
ОДЗ корня: подкоренное выражение должно быть >=0.
ОДЗ дроби: знаменатель не равен 0.
ОДЗ логарифма включает три условия: основание логарифма > 0, основание логарифма не равно 1, аргумент логарифма >0.

drtsv: Странно символы отобразились.
Ещё раз напишу.
ОДЗ корня: подкоренное выражение должно быть больше либо равно 0.
ОДЗ дроби: знаменатель не равен 0.
ОДЗ логарифма состоит из трёх условий: основание логарифма больше 0, основание логарифма не равно 1, аргумент логарифма больше 0.

Fimus: А к какому одз относятся неравенства из задания? не могу понять как находить в них его

drtsv: В данных примерах ОДЗ: любое число

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Українська мова, автор: Nazar503

Синонім слова поважати

2 года назад

Предмет: Немецкий язык, автор: дашкоо28

пожалуйста составьте небольшой рассказ на немецком языке о любимой музыке и муз группе

2 года назад

Предмет: Қазақ тiлi, автор: larisagrachova