ДАЮ 40 БАЛЛОВ
1. гипотенуза прямоугольного треугольника равна 41 а периметр равен 90. Найди больший катет
2.площадь прямоугольника равна 12, а длина диагонали в квадрате равна 40. найди ширину и длину прямоугольника.
Ответы
Ответ:
1. 40; 2. a=20√2, b=3 / 5√2 (насчёт ответа для второй задачи не уверена, я могла неправильно понять условие задачи)
Объяснение:
1.
1) с = 41
Р(периметр) = 90
Р(сумма длин всех сторон) = a + b + c
Р = а + b + 41
90 = а + b + 41
а = 90 - 41 - b
а = 49 - b.
2) По теореме Пифагора:
a² + b² = c²
(49 - b)² + b² = 41²
49² - 2×49×b + b² + b² = 41²
2401 - 98b + 2b² = 1681
2b² - 98b + 2401 - 1681 = 0
2b² - 98b + 720 = 0 (поделим всё на два)
b² - 49b + 360 = 0
D = b² - 4ac = (-49)² - 4×1×360 = 2401 - 1440 = 961 = 31²
b = (49 ± 31) / 2×1
b1 = (49+31) / 2= 40
b2 = (49-31) / 2 = 9.
3) Найдём сторону а:
а = 49 - b
а1 = 49 - 40 = 9
а2= 49 - 9 = 40
40 > 9
значит, больший катет равен 40.
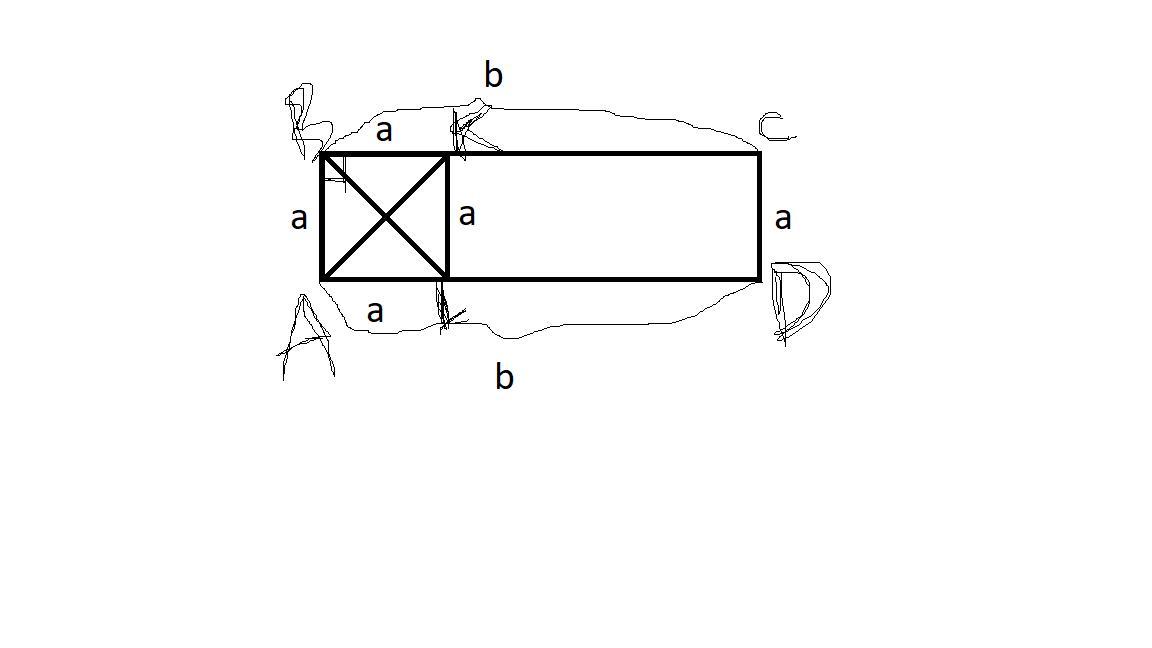
2. (для этой задачи я прикрепила рисунок)
Дано:
Sabcd = 12
AK=40
Найти: AB и BC
Решение:
1) Рассмотрим треугольник ABK:
AK=40
AB=BK=a (т.к. ABKL - квадрат)
По теореме Пифагора:
AB²+BK²=AK²
a²+a²=40²
2a²=1600
a²=1600/2
a²=800
a=√800= √400×2 = 20√2
2) Sabcd = a×b
b = Sabcd / a
b = 12 / 20√2 = 3 / 5√2